Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x0 là 
Cách giải: TXĐ: D = R
Ta có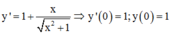 
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 0 là: 
- Gọi x 0 ; y 0 là tọa độ tiếp điểm.
- Ta có:
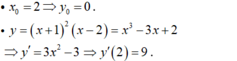
- Vậy phương trình tiếp tuyến cần tìm là:
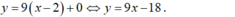
Chọn D.
Đáp án C
Ta có: y ' = − 4 x − 2 2 ⇒ y ' 1 = − 4 ; y 1 = − 3
Do đó PTTT tại điểm có hoành độ bằng 1 là: y = − 4 x − 1 − 3 = − 4 x + 1
a) \(y' = \left( {{x^3} - 3{x^2} + 4} \right)' = 3{x^2} - 6x\), \(y'\left( 2 \right) = {3.2^2} - 6.2 = 0\)
Thay \({x_0} = 2\) vào phương trình \(y = {x^3} - 3{x^2} + 4\) ta được: \(y = {2^3} - {3.2^2} + 4 = 0\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 0.(x - 2) + 0 = 0\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là y = 0
b) \(y' = \left( {\ln x} \right)' = \frac{1}{x}\), \(y'(e) = \frac{1}{e}\)
Thay \({x_0} = e\) vào phương trình \(y = \ln x\) ta được: \(y = \ln e = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = \frac{1}{e}.\left( {x - e} \right) + 1 = \frac{1}{e}x - 1 + 1 = \frac{1}{e}x\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = \frac{1}{e}x\)
c) \(y' = \left( {{e^x}} \right)' = {e^x},\,\,y'(0) = {e^0} = 1\)
Thay \({x_0} = 0\) vào phương trình \(y = {e^x}\) ta được: \(y = {e^0} = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 1.\left( {x - 0} \right) + 1 = x + 1\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = x + 1\)
Đáp án là A.
y ' = x 2 + 2 x ⇒ y ' ' = 2 x + 2 = 0 ⇔ x = − 1 ⇒ y ' − 1 = − 1
Phương trình tiếp tuyến của (C) tại − 1 ; − 4 3 là:
y = − 1 x + 1 − 4 3 = − x − 7 3 .
- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm.
- Ta có:
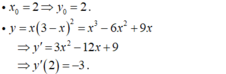
- Vậy phương trình tiếp tuyến cần tìm là :
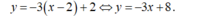
Chọn A
Chọn C