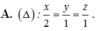
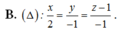
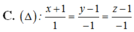
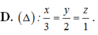
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Phương pháp giải:
Ứng dụng của tích có hướng để tìm vectơ pháp tuyến của mặt phẳng. Phương trình mặt phẳng đi qua M ( x 0 ; y 0 ; z 0 ) và có VTPT
Lời giải:
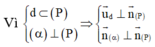
Vậy phương trình mặt phẳng (P): 2x-3y-z+7=0
Đáp án B
Vì đường thẳng vuông góc với (P) nên nhận vecto pháp tuyến của (P) là (1; 3; -1) làm vecto chỉ phương nên chỉ có đáp án B hoặc C
Thay điểm A (2;3;0) vào thì chỉ có đáp án B thỏa mãn
Đáp án C
Mặt phẳng cần tìm vuông góc với ∆ nên nhận vecto chỉ phương của ∆ là (3; -2; 1) làm vecto pháp tuyến.
Phương trình mặt phẳng cần tìm là: 
Đáp án C
Δ : x − 1 3 = y + 2 − 2 = z − 3 1 có véc tơ chỉ phương là u → = 3 ; − 2 ; 1
Phương trình mặt phẳng cần tìm đi qua M và vuông góc với đường thẳng
Δ : x − 1 3 = y + 2 − 2 = z − 3 1 nên nhận u → = 3 ; − 2 ; 1 làm véc tơ pháp tuyến có phương trình là:
3
x
−
3
−
2
y
+
1
+
1
z
−
1
=
0
⇔
3
x
−
2
y
+
z
−
12
=
0
Chọn đáp án C