Cho d : x - 5 2 = y + 1 - 2 = z - 7 1 , A 4 ; - 3 ; 2 , O 0 ; 0 ; 0 . Gọi A', O' lần lượt là hình chiếu vuông góc của A và O xuống (d). Tính độ dài A'O'.
![]()
![]()
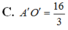
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)
\(\Rightarrow\dfrac{a+b}{c+a}=\dfrac{a-b}{c-a}=\dfrac{a+b+a-b}{c+a+c-a}=\dfrac{a}{c}\) (T/c dãy tỷ số = nhau)
\(\Rightarrow\dfrac{a+b}{c+a}=\dfrac{a}{c}\Rightarrow c\left(a+b\right)=a\left(c+a\right)\)
\(\Rightarrow ac+bc=ac+a^2\Rightarrow a^2=bc\)

a, x=5y/7thay vào x-y = 1
ta đc:
5y/7 - y=1
<=> -2y=7
<=> y=-7/2
=> x=-5/2

a\(\left(x-3\right)^2-\left(x+2\right)^2-5\left(\frac{1}{5}-7\right)=-30\)
=>(x-3-x-2)(x-3+x+2)-x+35=-30
=>-5(2x-1)-x+35=-30
=>-10x+5-x+35=-30
=>-11x+40=-30
=>-11x=-70 =>x=70/11
d)\(\left(x+3\right)^2-\left(x+5\right)\left(x-5\right)=2\)
\(=>\left(x+3\right)^2-x^2+25=2\)
\(=>\left(z+3-z\right)\left(z+3+z\right)+25=2\)
\(=>3\left(2z+3\right)+25-2=0\)
\(=>6z+9+23=0\)
\(=>6x+32=0=>6x=-32=>x=-\frac{16}{3}\)
e)\(3\left(x+2\right)^2+\left(2x-1\right)^2-7\left(x+3\right)\left(x-3\right)=36\)
\(=>3\left(x^2+4x+4\right)+\left(4x^2-4x+1\right)-7\left(x^2-9\right)=36\)
\(=>3x^2+12x+12+4x^2-4x+1-7x^2+63\)
\(=>8x+76=36=>8x=36-76=>x=-40\div8=-5\)
g)\(\left(x-1\right)\left(x^2+x+1\right)-x\left(x+2\right)\left(x-2\right)=5\)
\(=>x^3-1-x\left(x^2-4\right)=5=>x^3-1-x^3+4x=5\)
\(=>4x-1=5=>4x=6=>x=\frac{3}{2}\)

a,
\(\left|x+\dfrac{9}{2}\right|\ge0\forall x\\ \left|y+\dfrac{4}{3}\right|\ge0\forall y\\ \left|z+\dfrac{7}{2}\right|\ge0\forall z\\ \Rightarrow\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\ge0\forall x,y,z\)
Mà
\(\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|\le0\\ \Rightarrow\left|x+\dfrac{9}{2}\right|+\left|y+\dfrac{4}{3}\right|+\left|z+\dfrac{7}{2}\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{9}{2}\right|=0\\\left|y+\dfrac{4}{3}\right|=0\\\left|z+\dfrac{7}{2}\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x+\dfrac{9}{2}=0\\y+\dfrac{4}{3}=0\\z+\dfrac{7}{2}=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-9}{2}\\y=\dfrac{-4}{3}\\z=\dfrac{-7}{2}\end{matrix}\right.\)
Vậy \(x=\dfrac{-9}{2};y=\dfrac{-4}{3};z=\dfrac{-7}{2}\)
d,
\(\left|x+\dfrac{3}{4}\right|\ge0\forall x\\ \left|y-\dfrac{1}{5}\right|\ge0\forall y\\ \left|x+y+z\right|\ge0\forall x,y,z\\ \Rightarrow\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|\ge0\forall x,y,z\)
Mà
\(\left|x+\dfrac{3}{4}\right|+\left|y-\dfrac{1}{5}\right|+\left|x+y+z\right|=0\\ \Rightarrow\left\{{}\begin{matrix}\left|x+\dfrac{3}{4}\right|=0\\\left|y-\dfrac{1}{5}\right|=0\\\left|x+y+z\right|=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x+\dfrac{3}{4}=0\\y-\dfrac{1}{5}=0\\x+y+z=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\x+y+z=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\\dfrac{-3}{4}+\dfrac{1}{5}+z=0\end{matrix}\right.\\\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\\dfrac{-11}{20}+z=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{4}\\y=\dfrac{1}{5}\\z=\dfrac{11}{20}\end{matrix}\right.\)