Với gia trị nào của tham số m thì hàm số y = - 1 3 x 3 - m x 2 + ( 2 m - 3 ) x - m + 2 nghịch biến trên ℝ ?
A. -3 ≤ m ≤ 1
B. m ≤ 1
A. m ≤ -3 hoặc m ≥ 1
D. -3 < m < 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: Để hàm số đồng biến khi x>0 thì m-1>0
hay m>1
b: Để hàm số nghịch biến khi x>0 thì 3-m<0
=>m>3
c: Để hàm số nghịch biến khi x>0 thì m(m-1)<0
hay 0<m<1
a, đồng biến khi m - 1 > 0 <=> m > 1
b, nghịch biến khi 3 - m < 0 <=> m > 3
c, nghịch biến khi m^2 - m < 0 <=> m(m-1) < 0
Ta có m - 1 < m
\(\left\{{}\begin{matrix}m-1< 0\\m>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

Đáp án B
Ta có y ' = 3 ( m - 1 ) + ( 2 m + 1 ) sin x để hàm số nghịch biến trên ℝ thì y ' ≤ 0 với mọi x xét BPT
3 ( m - 1 ) + ( 2 m + 1 ) sin x ≤ 0 Nếu m = - 1 2 BPT luôn đúng. Với m > - 1 2 BPT ⇔ sin x ≤ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≥ 1 ⇒ - 1 2 < m ≤ 2 5 . Với m < - 1 2 BPT ⇔ sin x ≥ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≤ - 1 ⇒ m < - 1 2
Kết hợp hai trường hợp ta có m ≤ 2 5
Chọn A
Tập xác định: D = ℝ . Ta có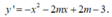 Để hàm số nghịch biến trên
ℝ
thì
Để hàm số nghịch biến trên
ℝ
thì