chứng tỏ phân số n3+2n / n4+3n2+1 tối giản
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
2
1 tháng 4 2016
GỌI Đ LÀ ƯC (2N+1/3N+2)
=>2N+2 CHIA HẾT CHO Đ=>3(2N+3) CHIA HẾT CHO Đ
=>3N+2CHIA HẾT CHO Đ=>2(3N+4) CHIA HẾT CHO DD
=>(6N+3)-(6N+4) CHIA HẾT CHO Đ
=>1 CHIA HẾT CHO Đ
=>Đ=1
=>2N+1/3N+2 LÀ P/S TỐI GIẢN
PT
1
25 tháng 2 2017
Gọi d ∈ ƯCLN (2n + 1; 2n + 3) nên ta có :
2n + 1 ⋮ d và 2n + 3 ⋮ d
=> (2n + 3) - (2n + 1) ⋮ d
=> 2n + 3 - 2n - 1 ⋮ d
=> 2 ⋮ d => d = { 1; 2 }
Mà 2n + 1 và 2n + 3 là các số lẻ nên ko có ước là 2
=> d = 1
Vì ƯCLN (2n + 1; 2n + 3) = 1 => \(\frac{2n+1}{2n+3}\) là phân số tối giản
22 tháng 2 2023
a: Gọi d=ƯCLN(2n+7;n+3)
=>2n+7-2n-6 chia hết cho d
=>1 chia hết cho d
=>d=1
=>phân số tối giản
b: Gọi d=ƯCLN(5n+7;2n+3)
=>10n+14-10n-15 chia hết cho d
=>-1 chia hết cho d
=>d=1
=>ĐPCM
c: Gọi d=ƯCLN(2n+1;3n+1)
=>6n+3-6n-2 chia hết cho d
=>1 chia hết cho d
=>d=1
=>ĐPCM
ND
3
11 tháng 4 2023
gọi d là ƯCLN(2n+1;3n+2).theo bài ra ta có:
2n+1 chia hết cho d=>6n+3 chia hết cho d
3n+2 chia hết cho d=>6n+4 chia hết cho d
=>1 chia hết cho d=>d=1
vậy ...
VN
Võ Ngọc Phương
VIP
11 tháng 4 2023
Gọi d ϵ ƯCLN\(\left(\dfrac{2n+1}{3n+2}\right)\)
Nên 2n+1⁝ d và 3n+2 ⁝ d
⇒ 3(2n+1) ⁝ d và 2(3n+2)
⇒ 6n+3 ⁝ d và 6n+4 ⁝ d
⇒ ( 6n+4 - 6n+3) ⁝ d
⇒ 1⁝ d
⇒ d= 1
Vậy:..
Chúc bạn học tốt
31 tháng 7 2021
Gọi a là ƯCLN(2n+1;3n+2)
Ta có 2n+1 chia hết cho a nên 3(2n+1) cũng chia hết cho a hay 6n+3 cũng chia hết cho a
Ta có 3n+2 chia hết cho a nên 2(3n+2) cũng chia hết cho a hay 6n+4 cũng chia hết cho a
Ta suy ra [(6n+4)-(6n+3)] chia hết cho a
(6n+4-6n-3) chia hết cho a
1 chia hết cho a
31 tháng 7 2021
Gọi \(d\inƯC\left(2n+1;3n+2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}2n+1⋮d\\3n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6n+3⋮d\\6n+4⋮d\end{matrix}\right.\)
\(\Leftrightarrow1⋮d\)
\(\Leftrightarrow d\in\left\{1;-1\right\}\)
\(\LeftrightarrowƯCLN\left(2n+1;3n+2\right)=1\)
hay \(\dfrac{2n+1}{3n+2}\) là phân số tối giản
RA
4
30 tháng 4 2019
Gọi d là ƯCLN ( 2n + 1 ; 3n + 2 )( d thuộc N* )
=> 2n + 1 chia hết cho d ; 3n + 2 chia hết cho d
=> 3( 2n + 1 ) chia hết cho d ; 2( 3n + 2 ) chia hết cho d
=> 6n + 3 chia hết cho d ; 6n + 4 chia hết cho d
=> ( 6n + 4 ) - ( 6n + 3 ) chia hết cho d
=> 6n + 4 - 6n - 3 chia hết cho d
=> 1 chia hết cho d
Mà d thuộc N* => d = 1
=> ƯCLN( 2n + 1 ; 3n + 2 ) = 1
Chứng tỏ phân số 2n + 1/3n + 2 tối giản
NH
5
1 tháng 5 2015
GIẢI TIẾP : Từ [1] và [2] => 1 chia hết cho d => d = 1
=> dpcm
cho minh cai dung
1 tháng 5 2015
gọi d là ƯCLN(2n+1;3n+2).theo bài ra ta có:
2n+1 chia hết cho d=>6n+3 chia hết cho d
3n+2 chia hết cho d=>6n+4 chia hết cho d
=>1 chia hết cho d=>d=1
=>ĐPCM
DN
2
26 tháng 4 2016
Gọi d là ƯCLN(2n+1;3n+2)
Ta có 2n+1 chia hết cho d nên 3(2n+1) cũng chia hết cho d hay 6n+3 cũng chia hết cho d
3n+2 chia hết cho d nên 2(3n+2) cũng chia hết cho d hay 6n+4 cũng chia hết cho d
Ta suy ra [(6n+4)-(6n+3)] chia hết cho d
(6n+4-6n-3) chia hết cho d
1 chia hết cho d
nên d=1
Vì ƯCLN(2n+1;3n+2)=1 nên 2n+1 phần 3n+2 là phân số tối giản (tick nhé 
)
26 tháng 4 2016
Gọi a là ước chung lớn nhất của \(\frac{2n+1}{3n+2}\)
suy ra 2n+1 chia hết cho a
3n+2 chia hết cho a
nên 3.(2n+1) chia hết cho a
2(3n+2) chia hết cho a
=> 6n+3 chia hết cho a
6n+4 chia hết cho a
vậy (6n+4)-(6n+3) chia hết cho a
1 chia hết cho a
vậy a=1
=> phân số \(\frac{2n+1}{3n+2}\) là phân số tối giản.
8 tháng 4 2015
Ta đặt ƯCLN(n+1;2n+1)=d suy ra 1.(2n+1)-2.(n+1) chia hết cho d hay 1 chia hết cho b.
Vậy suy ra điều phải chứng minh.
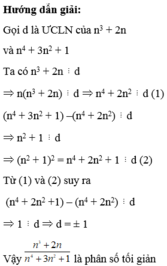
bn nhấn vào đúng 0 sẽ ra đáp án