Cho hình chóp có 20 cạnh. Tính số mặt của hình chóp đó.
A. 20
B. 10
C. 12
D. 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
13 tháng 8 2018
Đáp án B
Giả sử đáy của hình chóp có n cạnh => 2n = 20 <=> n = 10 => số mặt là 10 + 1 = 11.
PT
1
CM
4 tháng 12 2018
Đáp án B
Giả sử đáy của hình chóp có n cạnh ⇒ 2 n = 20 ⇔ n = 10 ⇒ số mặt là 10 + 1 = 11
PT
1
CM
23 tháng 11 2018
Chọn D.
Gọi số mặt của hình chóp là n
=> số mặt bên của hình chóp là n-1. Suy ra số cạnh của đa giác đáy hình chóp có n-1 cạnh.
Vậy số cạnh bên của hình chóp là 20-(n-1)=21-n
Mặt khác số cạnh bên của hình chóp bằng số mặt bên của hình chóp nên ta có
=> n-1=21-n=> n=11
PT
1
CM
20 tháng 3 2017
Chọn B
Số cạnh bên của hình chóp bằng số cạnh đáy.
Suy ra số cạnh bên của hình chóp là: 20 2 = 10 cạnh.
Vậy hình chóp có 10 mặt bên và 1 mặt đáy.
PT
1
CM
29 tháng 1 2019
Chọn đáp án B
Số cạnh bên của hình chóp bằng số cạnh đáy
Suy ra số cạnh bên của hình chóp là: 20 2 = 10 cạnh
Vậy hình chóp có 10 mặt bên và 1 mặt đáy
CM
26 tháng 4 2019
Đáp án là C
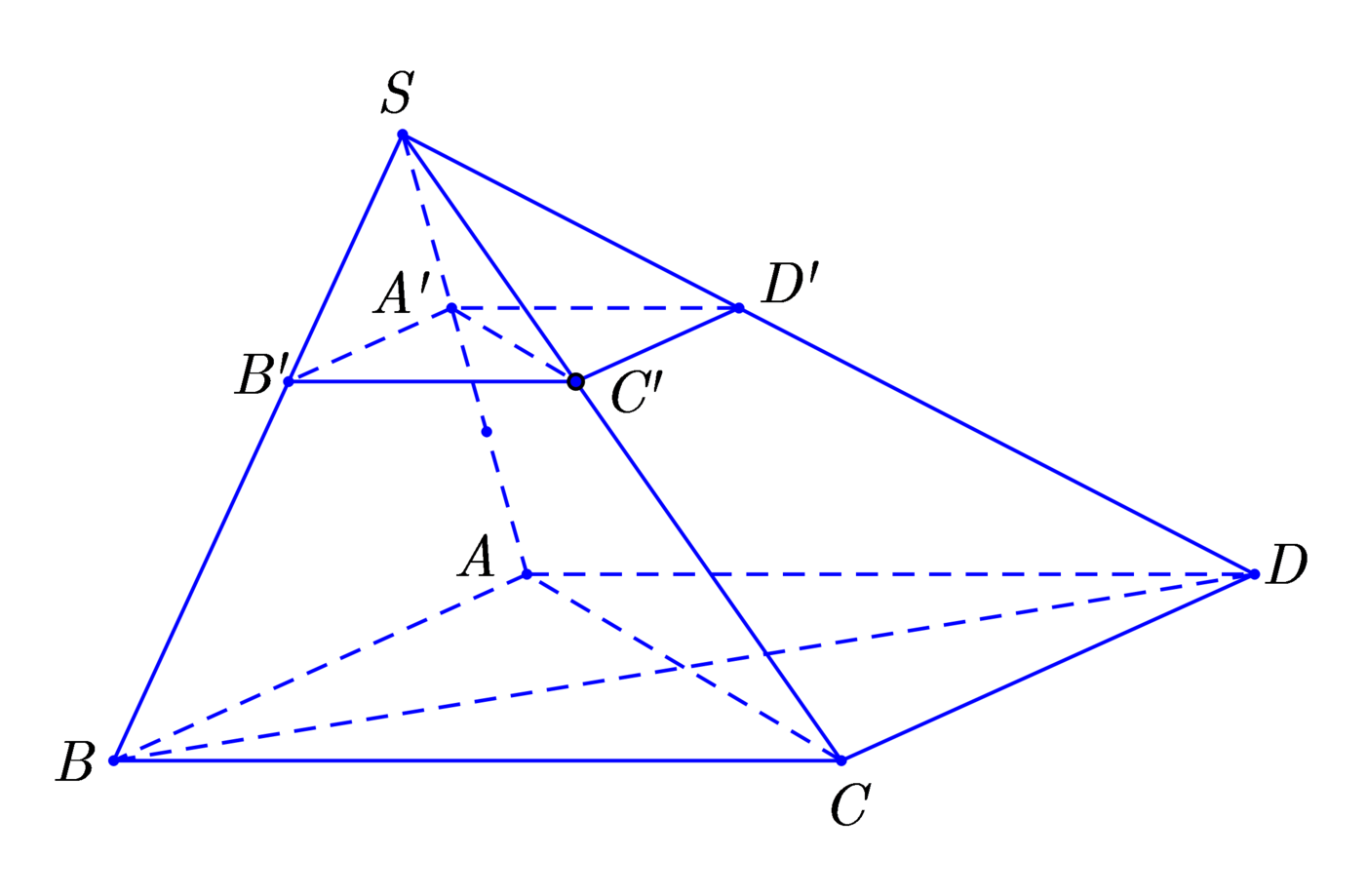
V S . A ' B ' C ' V S . A B C = 1 27 ⇒ V S . A ' B ' C ' = 1 27 V S . A B C ⇒ V S . A B C D = 2 V S . A ' B ' C ' = 2 27 . 1 2 V S . A B C D = V 27 .
PT
1
CM
29 tháng 11 2018
Chọn A.
Chóp n- giác bao gồm n cạnh bên và đáy là n-giác Þ Có tất cả 2n cạnh.
Theo bài ra ta có: 2n = 10 Û n = 5. Suy ra hình chóp có 10 cạnh là chóp ngũ giác, có 5 mặt bên và 1 mặt đáy
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)
Chọn D.
Gọi số mặt của hình chóp là n n ∈ N *
=> số mặt bên của hình chóp là n-1 . Suy ra số cạnh của đa giác đáy hình chóp có n-1 cạnh.
Vậy số cạnh bên của hình chóp là 20-(n-1)=21-n
Mặt khác số cạnh bên của hình chóp bằng số mặt bên của hình chóp nên ta có:
=> n-1=21-n => n=11