Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Gọi số mặt của hình chóp là n n ∈ N *
=> số mặt bên của hình chóp là n-1 . Suy ra số cạnh của đa giác đáy hình chóp có n-1 cạnh.
Vậy số cạnh bên của hình chóp là 20-(n-1)=21-n
Mặt khác số cạnh bên của hình chóp bằng số mặt bên của hình chóp nên ta có:
=> n-1=21-n => n=11

Chọn đáp án B
Số cạnh bên của hình chóp bằng số cạnh đáy
Suy ra số cạnh bên của hình chóp là: 20 2 = 10 cạnh
Vậy hình chóp có 10 mặt bên và 1 mặt đáy

Đáp án là C
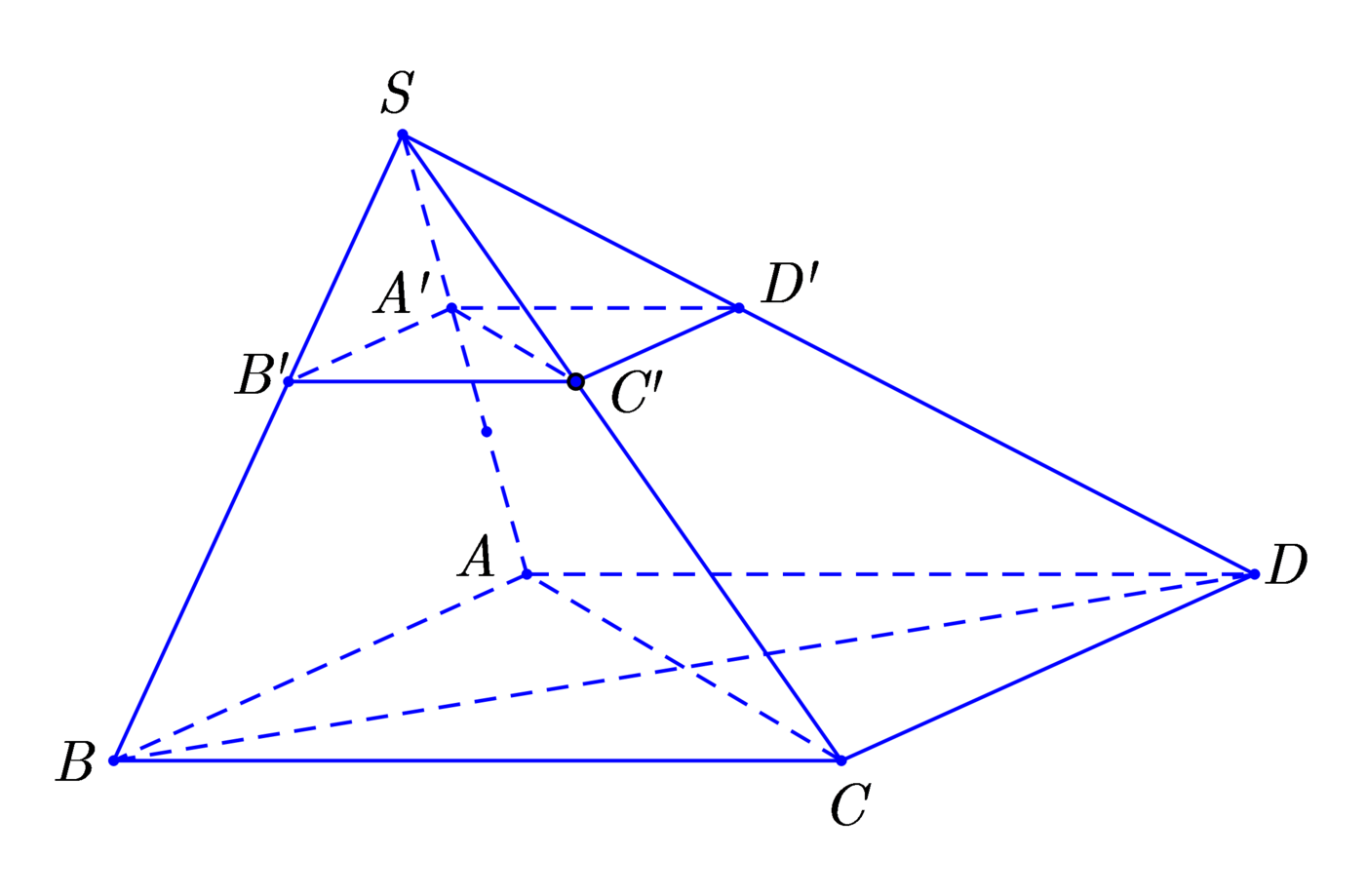
V S . A ' B ' C ' V S . A B C = 1 27 ⇒ V S . A ' B ' C ' = 1 27 V S . A B C ⇒ V S . A B C D = 2 V S . A ' B ' C ' = 2 27 . 1 2 V S . A B C D = V 27 .

Chọn A.
Chóp n- giác bao gồm n cạnh bên và đáy là n-giác Þ Có tất cả 2n cạnh.
Theo bài ra ta có: 2n = 10 Û n = 5. Suy ra hình chóp có 10 cạnh là chóp ngũ giác, có 5 mặt bên và 1 mặt đáy

Đáp án C
Dễ thấy hình chóp S.A'B'C'D' đồng dạng với hình chópS.ABCD theo tỷ số k = 1 3
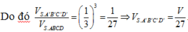

Đáp án D
Hình chóp có 10 cạnh thì tức là hình chóp có đáy có 10 2 = 5 cạnh. Tức là đáy có 5 điểm ở đáy kết hợp với 1 đỉnh, vậy hình chóp này có 6 điểm.

Đáp án D
Hình chóp có 10 cạnh thì tức là hình chóp có đáy có 10 2 = 5 cạnh. Tức là đáy có 5 điểm ở đáy kết hợp với 1 đỉnh, vậy hình chóp này có 6 điểm.

Đáp án B.
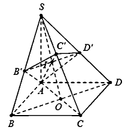
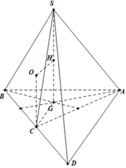
Gọi O là tâm của hình vuông ABCD, nối S O ∩ B ' D ' = I .
Và nối AI cát SC tại C’ suy ra mp (AB’D’) cắt SC tại C’.
Tam giác SAC vuông tại A, có S C 2 = S A 2 + A C 2 = 6 a 2 ⇒ S C = a 6 .
Ta có B C ⊥ S A B ⇒ B C ⊥ A B ' và S B ⊥ A B ' ⇒ A B ' ⊥ S C .
Tương tự A D ' ⊥ S C suy ra S C ⊥ ( A B ' D ' ) ≡ ( A B ' C ' D ' ) ⇒ S C ⊥ A C ' .
Mà S C ' . S C = S A 2 ⇒ S C ' S C = S A 2 S C 2 = 2 3 và S B ' S B = S A 2 S B 2 = 4 5 .
Do đó V S . A B ' C ' = 8 15 V S . A B C = 8 30 V S . A B C D mà V S . A B C D = 1 3 . S A . S A B C D = 2 a 3 3 .
Vậy thể tích cần tính là V S . A B ' C ' D ' = 2 . V S . A B ' C ' = 16 a 3 45

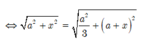

Đáp án B
Giả sử đáy của hình chóp có n cạnh ⇒ 2 n = 20 ⇔ n = 10 ⇒ số mặt là 10 + 1 = 11