Cho 2 số a > 0 , a ≠ 1 , b > 0 thỏa mãn hệ thức a 2 + b 2 = 4 a b . Đẳng thức nào sau đây đúng?
A. 2 log a a − b = log a 2 a b
B. 2 log a 4 a b = log a a 2 + log a b 2
C. 2 log a a + b = 1 + log a 6 b
D. 2 log a 4 a b = 2 log a a + b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để ý rằng 1 < a < b < c nên log a b > 1. Khi đó nếu xét cùng các cơ số a và b thì
log a log a b > log b log a b > 0
Do 1 < a < b < c nên
log c a < 1 ⇒ 0 > log c log c a > log b log c a
Từ đó suy ra
log a log a b + log b log b c + log c log c a > log b log a b . log b c . log c a = log b 1 = 0
Đáp án A

Ta có: \(a^3+b^3+3\left(a^2+b^2\right)+4\left(a+b\right)+4=0\)
<=> \(\left(a+b\right)^3-3ab\left(a+b\right)+3\left(a+b\right)^2-6ab+4\left(a+b\right)+4=0\)
<=> \(\left[\left(a+b\right)^3+2\left(a+b\right)^2\right]-3ab\left(a+b+2\right)+\left(a+b\right)^2+4\left(a+b\right)+4=0\)
<=> \(\left(a+b\right)^2\left(a+b+2\right)-3ab\left(a+b+2\right)+\left(a+b+2\right)^2=0\)
<=> \(\left(a+b+2\right)\left(\left(a+b\right)^2-3ab+a+b+2\right)=0\)
<=> \(\left(a+b+2\right)\left(a^2+b^2-ab+a+b+2\right)=0\)(1)
Có: \(a^2+b^2-ab+a+b+2=\frac{1}{2}\left[\left(a-b\right)^2+\left(a+1\right)^2+\left(b+1\right)^2\right]+1>0\)
=> (1) <=> a + b + 2 = 0 <=> a + b = -2
Thế vào tìm M .
Cố gắng học tốt giúp đỡ mọi người nhiều hơn nhé! :))))

\(\frac{1}{x^2-4}=\frac{a}{x-2}+\frac{b}{x+2}\) \(\left(\text{*}\right)\)
\(ĐKXĐ:\) \(x\notin\left\{-2;2\right\}\)
Thực hiện phép cộng ở vế phải của \(\left(\text{*}\right)\), khi đó,
\(\frac{a\left(x+2\right)+b\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{ax+2a+bx-2b}{\left(x-2\right)\left(x+2\right)}=\frac{\left(a+b\right)x+2\left(a-b\right)}{\left(x-2\right)\left(x+2\right)}\)
Đồng nhất phân thức trên với phân thức \(\frac{1}{x^2-4}\), tức \(\frac{1}{\left(x-2\right)\left(x+2\right)}\), ta được:
\(a+b=0\) \(a=\frac{1}{4}\)
\(\Leftrightarrow\)
\(2\left(a-b\right)=1\) \(b=-\frac{1}{4}\)
Vậy, \(\frac{1}{x^2-4}=\frac{\frac{1}{4}}{x-2}+\frac{\left(-\frac{1}{4}\right)}{x+2}\)

Chọn D
Cho 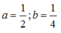 ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
Đáp án C
Ta có a 2 + b 2 = 4 a b ⇔ a 2 + 2 a b + b 2 = 6 a b ⇔ a + b 2 = 6 a b
log a a + b 2 = log a 6 a b ⇔ 2 log a a + b = log a a + log a 6 b = 1 + log a 6 b