Tìm tất cả các giá trị thực của m để bất phương trình x 2 - 1 x - 1 x 3 + x 2 - x 2 2 - m + x 2 - 1 x - 1 ≥ 0 , ∀ x ∈ ℝ
A. m ≤ 2
B. m ≤ - 1 4
C. m ≤ 6
D. m ≤ 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


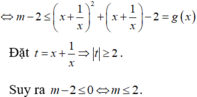


Đáp án C.
Bất phương trình ⇔ log 2 5 x - 1 1 + log 2 5 x - 1 ≥ m
Đặt t = log 2 5 x - 1 , do x ≥ 1 ⇒ t ∈ [ 2 ; + ∞ )
Bất phương trình t 2 + t ≥ m ⇔ f ( t ) ≥ m
Với f ( t ) = t 2 + t , f ' ( t ) = 2 t + 1 > 0 với t ∈ [ 2 ; + ∞ ) nên hàm số f ( t ) đồng biến nên min ( t ) = f ( 2 ) = 6
Do đó theo bài ra để bất phương trình có nghiệm x ≥ 1 thì m ≤ min f ( t ) ⇔ m ≤ 6

Để bất phương trình luôn có nghiệm thì
\(\left\{{}\begin{matrix}\left(m-1\right)^2-4\cdot1\cdot5< 0\\1>=0\end{matrix}\right.\Leftrightarrow\left(m-1\right)^2< 20\)
\(\Leftrightarrow-2\sqrt{5}+1< x< 2\sqrt{5}+1\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2>0\left(luôn-đúng\right)\\\Delta'< 0\end{matrix}\right.\) \(\Leftrightarrow\left(m+1\right)^2-\left(m^2+2\right)< 0\Leftrightarrow2m-1< 0\Leftrightarrow m< \dfrac{1}{2}\)