Gọi M là giá trị lớn nhất của hàm số f ( x ) = 6 x 2 - 6 x + 12 + 6 x - x 2 - 4 . Tính tích các nghiệm của phương trình f(x)=M.
A. -6
B. 3
C. -3
D. 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
31 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
CM
4 tháng 5 2019
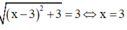
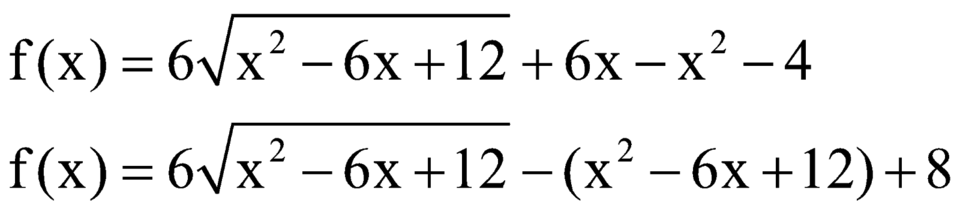
Đặt 
khi đó ta có 
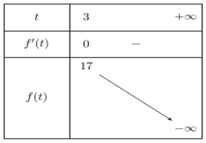
Ta có 
BBT:
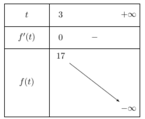
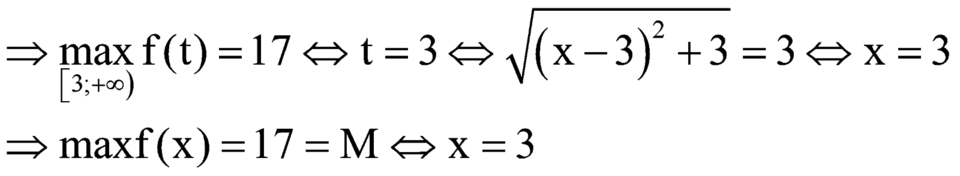
Vậy phương trình 
có nghiệm duy nhất x=3, do đó tích các nghiệm của chúng bằng 3.
Chọn B
CM
18 tháng 12 2018
Đáp án A
Phương pháp: Đặt 
Cách giải: Đặt 
Khi đó ta có 
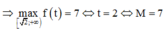
Khi đó tích hai nghiệm của phương trình này bằng -1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)
CM
8 tháng 10 2019
f ( x ) = 2 x 3 + 3 x 2 - 1 ⇒ f ' ( x ) = 6 x 2 + 6 x ; f ' ( x ) = 0 ⇔ [ x = 0 ( k t m ) x = - 1 ( t m )
Hàm số f(x) liên tục trên - 2 ; - 1 2 ,
có f ( - 0 ) = - 5 ; f ( - 1 ) = 0 ; f - 1 2 = - 1 2
⇒ m = m i n - 2 ; - 1 2 f ( x ) = - 5 ; M = m a x - 2 ; - 1 2 f ( x ) = 0 ⇒ P = M - m = 5
Chọn đáp án C.
20 tháng 7 2023
Ta có:
Khi \(x\in\left[-3;0\right]\) thì \(f\left(x\right)\in\left[-4;5\right]\) (dùng BBT)
Lại có:
\(y=f\left(f\left(x\right)\right)=f^2\left(x\right)+6f\left(x\right)+5\)
Khi \(f\left(x\right)\in\left[-4;5\right]\) thì \(f\left(f\left(x\right)\right)\in\left[-4;60\right]\) (dùng BBT)
Do đó, \(m=-4\Leftrightarrow f\left(x\right)=-3\Leftrightarrow x=-2\)
và \(M=60\Leftrightarrow f\left(x\right)=5\Leftrightarrow x=0\)
\(\Rightarrow S=m+M=-4+60=56\)
CM
16 tháng 3 2018
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2