Khi triển A= = . Biết rằng . Hỏi bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

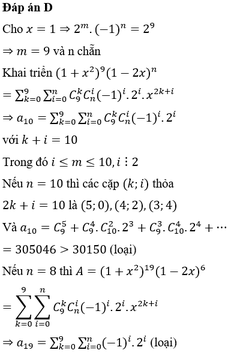
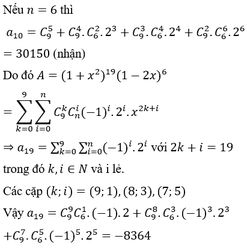

a: \(A=\left(\dfrac{1}{x-2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x+2}\right)\cdot\dfrac{2-x}{x}\)
\(=\dfrac{x+2+2x+x-2}{\left(x-2\right)\cdot\left(x+2\right)}\cdot\dfrac{-\left(x-2\right)}{x}\)
\(=\dfrac{-4x}{x\left(x+2\right)}=\dfrac{-4}{x+2}\)
b: Ta có: 2x+x=0
=>3x=0
hay x=0(loại)
c: Để A=1/2thì \(\dfrac{-4}{x+2}=\dfrac{1}{2}\)
=>x+2=-8
hay x=-10
d: Để A là số nguyên dương thì \(\left\{{}\begin{matrix}x>-2\\x+2\in\left\{1;-1;2;-2;4;-4\right\}\end{matrix}\right.\Leftrightarrow x\in\left\{-1;0;2\right\}\)

Cho biểu thức: bn viết ko rõ lắm , bn xem đề mk viết lại có đg ko nhé , r mk lm cho
\(a=\dfrac{2x}{x+3}-\dfrac{x+1}{3-x}-\dfrac{3-11x}{x^2-9}\)
Bài 1:
\(A=\dfrac{1}{x-y}+\dfrac{1}{x+y}+\dfrac{2x}{x^2+y^2}+\dfrac{4x^3}{x^4+y^4}+\dfrac{8x^7}{x^8+y^8}\)
\(A=\dfrac{2x}{x^2-y^2}+\dfrac{2x}{x^2+y^2}+\dfrac{4x^3}{x^4+y^4}+\dfrac{8x^7}{x^8+y^8}\)
\(A=\dfrac{4x^3}{x^4-y^4}+\dfrac{4x^3}{x^4+y^4}+\dfrac{8x^7}{x^8+y^8}\)
\(A=\dfrac{8x^7}{x^8-y^8}+\dfrac{8x^7}{x^8+y^8}\)
\(A=\dfrac{16x^{15}}{x^{16}-y^{16}}\)

Xét khai triển:
\(\left(x+1\right)^n=C_n^0+C_n^1x+C_n^2x^n+C_n^3x^3+...+C_n^nx^n\)
Đạo hàm 2 vế:
\(n\left(x+1\right)^{n-1}=C_n^1+2C_n^2x+3C_n^3x^2+...+nC_n^nx^{n-1}\)
Thay \(x=1\) vào ta được:
\(n.2^{n-1}=C_n^1+2C_n^2+3C_n^3+...+nC_n^2=256n\)
\(\Rightarrow2^{n-1}=256=2^8\Rightarrow n=9\)
Câu 2:
\(\left(x-2\right)^{80}=a_0+a_1x+a_2x^2+a_3x^3+...+a_{80}x^{80}\)
Đạo hàm 2 vế:
\(80\left(x-2\right)^{79}=a_1+2a_2x+3a_3x^2+...+80a_{80}x^{79}\)
Thay \(x=1\) ta được:
\(80\left(1-2\right)^{79}=a_1+2a_2+3a_3+...+80a_{80}\)
\(\Rightarrow S=80.\left(-1\right)^{79}=-80\)

Bài 3:
\(3x^2+2x-1=0\)
\(\Leftrightarrow x^2+\dfrac{2}{3}x-\dfrac{1}{3}=0\)
\(\Leftrightarrow x^2+2.x.\dfrac{1}{3}+\dfrac{1}{9}-\dfrac{4}{9}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{3}\right)^2-\dfrac{4}{9}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{3}\right)^2=\dfrac{4}{9}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=\dfrac{2}{3}\\x+\dfrac{1}{3}=\dfrac{-2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-1\end{matrix}\right.\)
Vậy...

a:ĐKXĐ: x<>2; x<>-2; x<>0
\(A=\dfrac{x^2+x-2+3x-6-x^2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-2\right)}{4\left(x-2\right)}\)
\(=\dfrac{4x-8}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x}{4}\)
\(=\dfrac{4x}{4\left(x+2\right)}=\dfrac{x}{x+2}\)
b: Để A>0 thì x/x+2>0
=>x>0 hoặc x<-2
Để A<0 thì x/x+2<0
=>-2<x<0
Để A<-5 thì A+5<0
=>(x+5x+10)/(x+2)<0
=>(6x+10)/(x+2)<0
=>-2<x<-5/3
Để A>3 thì A-3>0
=>(x-3x-6)/(x+2)>0
=>(-2x-6)/(x+2)>0
=>(x+3)/(x+2)<0
=>-3<x<-2
c: Khi x=1 thì A=1/(1+2)=1/3
x^2-9=0
=>x=3 hoặc x=-3
Khi x=3 thì \(A=\dfrac{3}{3+2}=\dfrac{3}{5}\)
Khi x=-3 thì \(A=\dfrac{-3}{-3+2}=\dfrac{-3}{-1}=3\)
e: Để A là số nguyê thì \(x+2-2⋮x+2\)
=>\(x+2\in\left\{1;-1;2;-2\right\}\)
hay \(x\in\left\{-1;-3\right\}\)
