Cho tứ diện ABCD có AB=AC=ADvà B A C = B A D = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
A. 90 °
B. 45 °
C. 60 °
D. 30 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 3 2018
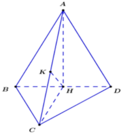
Ta có:
Xét ∆ A H C vuông tại H có đường cao KH ta có:
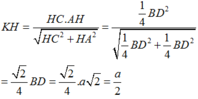
Chọn B.
20 tháng 5 2017
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó ABE.FDC là một lăng trụ đứng
Ta có :
\(S_{ABE}=\dfrac{1}{2}ab.\sin60^0=ab\dfrac{\sqrt{3}}{4}\)
\(V_{C.ABE}=\dfrac{1}{3}.\dfrac{\sqrt{3}}{4}ab.h=\dfrac{\sqrt{3}}{12}abh\)
Từ đó suy ra :
\(V_{A.BCD}=V_{A.BCE}=\dfrac{\sqrt{3}}{12}abh\)
Các tam giác ABC và ABD đều là tam giác cân có 1 góc bằng 600 (gt) nên ∆ A B C ; ∆ A B D là các tam giác đều.
Lấy N là trung điểm AB. Khi đó C N ⊥ A B ; D N ⊥ A B (tính chất tam giác đều)
⇒ A B ⊥ D C N ⇒ A B ⊥ D C
Nên góc giữa AB và CD là 90 ° .
Chọn đáp án A.