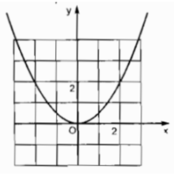
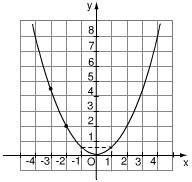
Parabol y = a x 2 trong hình vẽ có hệ số a là bao nhiêu?
A) 1
B) -1
C) 2
D) 1/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 Khi đốt khí axetilen (C₂H₂), số mol CO₂ và H₂O được tạo thành theo tỉ lệ là:
A 1 : 1
B 2 : 1
C 1 : 2
D 1 : 3
2 Axetilen có tính chất vật lý:
A là chất khí không màu, không mùi, ít tan trong nước, nặng hơn không khí.
B là chất khí không màu, mùi hắc, ít tan trong nước, nặng hơn không khí.
C là chất khí không màu, không mùi, tan trong nước, nhẹ hơn không khí.
D là chất khí không màu, không mùi, ít tan trong nước, nhẹ hơn không khí.
3 Ứng dụng nào sau đây “không” phải ứng dụng của etilen?
A Điều chế rượu etylic và axit axetic.
B Điều chế khí gas.
C Dùng để ủ trái cây mau chín.
D Điều chế PE.

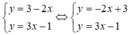
a) Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 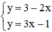 có nghiệm duy nhất.
có nghiệm duy nhất.
b) 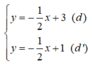
Xét (d): 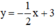 có a =
có a = 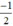 ; b = 3
; b = 3
(d’): 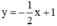 có a’ =
có a’ = 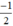 ; b’ = 1.
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 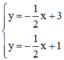 vô nghiệm.
vô nghiệm.
c) Ta có: 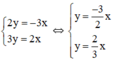
Xét (d): y = 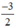 x có a =
x có a = 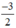 ; b = 0
; b = 0
(d’) : y = 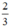 x có a’ =
x có a’ = 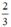 ; b’ = 0
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 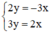 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Ta có:
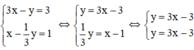
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 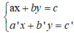
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.

Lời giải:
$|x+2|+2|x+2|=3$
$3|x+2|=3$
$|x+2|=1$
$\Rightarrow x+2=1$ hoặc $x+2=-1$
$\Rightarrow x=-1$ hoặc $x=-3$
Vậy có 2 giá trị nguyên của $x$ thỏa mãn
Đáp án C.

Bài giải:
a) Theo hình vẽ, ta lấy điểm A thuộc đồ thị có tọa độ là x = -2, y = 2. Khi đó ta được:
2 = a . (-2)2 suy ra a = 
b) Đồ thị có hàm số là y =  x2 . Tung độ của điểm thuộc parabol có hoành độ x = -3 là y =
x2 . Tung độ của điểm thuộc parabol có hoành độ x = -3 là y =  (-3)2 suy ra y =
(-3)2 suy ra y =  .
.
c) Các điểm thuộc parabol có tung độ là 8 là:
8 =  x2 ⇔ x2 = 16 ⇔ x = ± 4
x2 ⇔ x2 = 16 ⇔ x = ± 4
Ta được hai điểm và tọa độ của hai điểm đó là M(4; 8) và M'(-4; 8).
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đi qua điểm (2;2)
Do đó, tọa độ điểm (2;2) thỏa mãn phương trình hàm số:
Chọn đáp án D