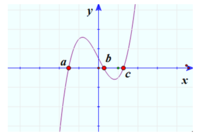
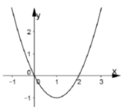
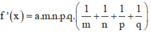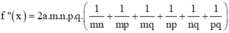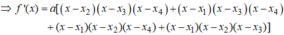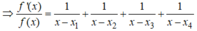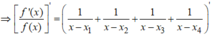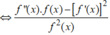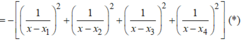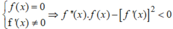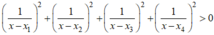Biết rằng đồ thị hàm số y = f(x) =
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
, cắt trục Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số ![]()
![]()
![]() cắt trục Ox tại bao nhiêu điểm?
cắt trục Ox tại bao nhiêu điểm?
A. 0
B. 4
C. 2
D. 6





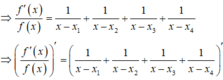
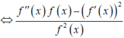
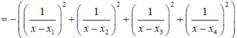
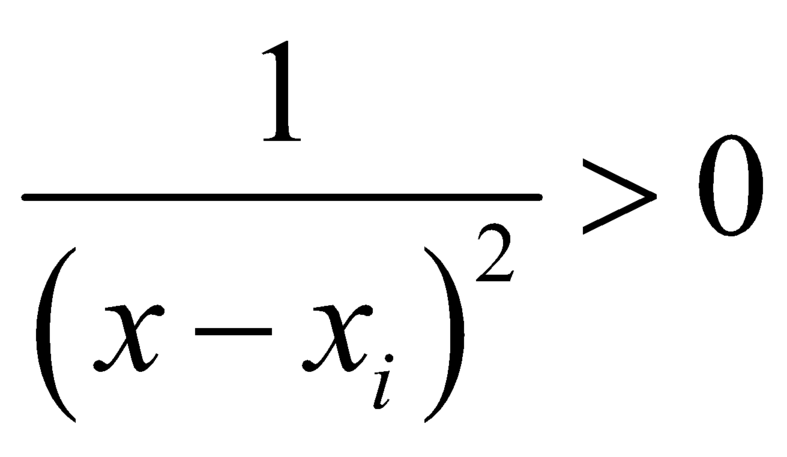 ,
,