Cho hình vuông ABCD cạnh a, trên đường thẳng vuông góc với (ABCD) tại A ta lấy điểm S di động. Hình chiếu vuông góc của A lên SB, SD lần lượt là H, K. Thể tích lớn nhất của tứ diện ACHK bằng A. ...

PT

Pham Trong Bach

2 tháng 1 2017

Cho hình vuông ABCD cạnh a, trên đường thẳng vuông góc với (ABCD) tại A ta lấy điểm S di động. Hình chiếu vuông góc của A lên SB, SD lần lượt là H, K. Thể tích lớn nhất của tứ diện ACHK bằng A. a 3 6 B. a 3 2 12 C. a 3 3 16 D. a 3 6 32 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

2 tháng 1 2017

Chọn đáp án C.

Đúng(0)

PT

Pham Trong Bach

2 tháng 4 2019

Cho hình vuông ABCD cạnh a trên đường thẳng vuông góc với (ABCD) tại A ta lấy điểm S di động. Hình chiếu vuông góc của A lên SB, SD lần lượt là H, K Thể tích lớn nhất của tứ diện ACHK bằng A. a 3 6 B. a 3 2 12 C. a 3 3 16 D. a 3 6 32 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

2 tháng 4 2019

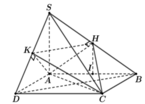
Tham khảo hình vẽ. Ta sẽ sử dụng công thức

Đặt SA = x (x > 0) Tính được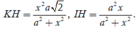

Chứng minh được

Khi đó

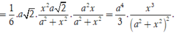
Xét hàm 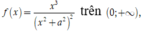ta có

Suy ra thể tích khối tứ diện lớn nhất bằng

Chọn C.

Đúng(0)

PT

Pham Trong Bach

5 tháng 10 2018

Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SA=a.Gọi H, K lần lượt là hình chiếu vuông góc của A trên SB, SD (tham khảo hình vẽ bên). Tang của góc tạo bởi đường thẳng SD và mặt phẳng (AHK) bằng A. 3 B. 2 C. 1 3 D. 3 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 10 2018

Chọn đáp án B

Đúng(0)

PT

Pham Trong Bach

13 tháng 8 2017

Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Tính diện tích của mặt cầu đó và tính thể tích khối cầu được tạo thành.

#Toán lớp 12

1

CM

Cao Minh Tâm

13 tháng 8 2017

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Gọi r là bán kính mặt cầu

ta có Giải sách bài tập Toán 12 | Giải sbt Toán 12

Vậy Giải sách bài tập Toán 12 | Giải sbt Toán 12

Đúng(0)

T

thanh

10 tháng 8 2020 - olm

Giúp em câu c với ạ*Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết rằng AB = SD = 3a, AD = SB = 4a, đường chéo AC vuông góc với mặt phẳng (SBD). Gọi H là hình chiếu vuông góc của S lên (ABCD) và K là giao điểm của AC và BD.a) Tính theo a thể tích khối chóp S.ABCD.b) Tính khoảng cách giữa hai đường thẳng BD và SA.c) Gọi P là hình chiếu vuông góc của K lên AB và Q là hình chiếu vuông...

Đọc tiếp

#Toán lớp 12

0

NT

Nhi Trần

10 tháng 2 2022

Cho hình chóp S ABCD, có đáy là hình vuông tâm O, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A lên SB, SC, SD.1.CMR : AH, AK cùng vuông góc với SC. Từ đó suy ra 3 đường thẳng AH, AI, AK cùng nằm trong một mặt phẳng. 2. Chứng minh rằng HK⊥(SAC) , HK ⊥...

Đọc tiếp

#Toán lớp 11

1

AM

Ami Mizuno

11 tháng 2 2022

Bạn vẽ hình giúp mình nha!

a. Ta có: \(\left\{{}\begin{matrix}BC\perp AB\left(ABCD.là.hình.vuông\right)\\BC\perp SA\left(SA\perp\left(ABCD\right)\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)

Có: \(\left\{{}\begin{matrix}BC\perp AH\left(cmt\right)\\AH\perp SB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (đpcm)

Chứng minh tương tự với AK, ta cũng có: \(AK\perp\left(SCD\right)\Rightarrow AK\perp SC\)

Có: \(\left\{{}\begin{matrix}AH\perp SC\\AK\perp SC\\AI\perp SC\end{matrix}\right.\) \(\Rightarrow\)SC vuông góc với mặt phẳng chứa A,H,I,K

Hay A,H,I,K cùng nằm trong một mặt phẳng

b. Có: \(SC\perp\left(HIK\right)\Rightarrow SC\perp HK\)

Xét \(\Delta SAB\) vuông tại A và \(\Delta SAD\) vuông tại A có: \(\left\{{}\begin{matrix}SA.là.cạnh.chung\\AB=AD\left(ABCD.là.hình.vuông\right)\end{matrix}\right.\)

\(\Rightarrow\)\(\Delta SAB\) = \(\Delta SAD\) \(\Rightarrow AH=AK\Rightarrow\dfrac{SH}{SB}=\dfrac{SK}{SD}\)

Áp dụng định lí Ta-let đảo ta có: HK//BD

Xét \(\Delta SBD\) có: SB=SD \(\Rightarrow\)\(\Delta SBD\) cân tại S

\(\Rightarrow\) SO vừa là đường trung tuyến vừa là đường cao

\(\Rightarrow\) \(SO\perp BD\)

Mà BD//HK

\(\Rightarrow\)\(SO\perp HK\)

Ta có: \(\left\{{}\begin{matrix}SO\perp HK\\SC\perp HK\end{matrix}\right.\) \(\Rightarrow HK\perp\left(SAC\right)\) (đpcm) \(\Rightarrow HK\perp AI\) (đpcm)

Đúng(2)

PT

Pham Trong Bach

18 tháng 3 2019

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA = a 2 . Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng A. 45 ° B. 60 ° C. 90 ° ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

18 tháng 3 2019

Đáp án B

Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A

Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C

Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3

⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .

Đúng(0)

DN

Đinh Ngọc Ánh

23 tháng 10 2021

sao suy ra được góc giữa SB; AMN = 60 ạ?

Đúng(0)

NM

Nguyễn Minh Anh

9 tháng 3 2019 - olm

Cho hình vuông ABCD, O là giao điểm hai đường chéo AC và BD . Trên đường thẳng vuông góc với mp(ABCD) tại B, lấy điểm S và nối S với A,B,C,D a)Chứng minh mp(SAC) vuông góc mp(SBD)

b) gọi m,n,p,q lần lượt là trung điểm của sa ,sb,sc,sd .chứng minh mp(mnpq)//mp(abcd)

c)tứ giác mnpq là hình gì? tính diện tích của tứ giác khi biết ab=a

#Toán lớp 8

0

NT

Nguyễn Thị Bích Ngọc

5 tháng 4 2018 - olm

cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.

Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA

#Toán lớp 9

0

NT

Nguyễn Thị Bích Ngọc

5 tháng 4 2018 - olm

cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với mp (ABCD), SD=a.căn 3. Gọi M và N lần lượt là hình chiếu của a lên SD và SB.

Tìm giao điểm K giữa SC và (AMN) và tính diện tích của MKNA

#Toán lớp 9

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP