Trong không gian với hệ tọa độ Oxyz, cho ba điểm và Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy AD và
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 nên B là trung điểm của AM.


Chọn C.
Phương pháp: Hai véc tơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau.


Đáp án là D.
+ Gọi H x ; y ; z là chân đường phân giác trong góc A của Δ A B C .
Ta có: H B → H C → = − A B A C = − 2
⇔ H B → = − 2 H C → ⇒ H − 5 3 ; 8 3 ; 0 ⇒ A H = 2 74 3 .


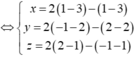
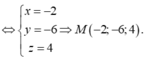

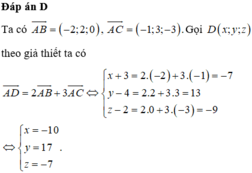


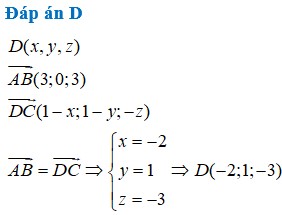
Đáp án D
Vì ABCD là hình thang ⇒ A D / / B C ⇒ u → A D = u → B C = − 5 ; − 2 ; 1
=>Phương trình đường thẳng AD là x + 2 − 5 = y − 3 − 2 = z − 1 1 ⇒ D − 5 t − 2 ; − 2 t + 3 ; t + 1
Ta có S A B C D = 3 S Δ A B C ⇔ S Δ A B C + S Δ A C D = 3 S Δ A B C ⇔ S Δ A C D = 2 S Δ A B C
Mà diện tích tam giác ABC là S Δ A B C = 1 2 A B ¯ ; A C ¯ = 341 2 ⇒ S Δ A C D = 341
Mặt khác A D ¯ ; A C ¯ = 341 t 2 ⇒ 1 2 341 t 2 = 341 ⇔ t = 2 t = − 2 ⇒ D − 12 ; − 1 ; 3 D 8 ; 7 ; − 1
Vì ABCD là hình thang → D − 12 ; − 1 ; 3