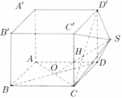
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD, S là điểm đối xứng với O qua CD’ (như hình vẽ). Thể tích của khối đa diện ABCDSA’B’C’D’ bằng
A. 2 a 3 3
B. 3 a 3 2
C. 7 a 3 6
D. 4 a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Ta có
![]()
Vì S là điểm đối xứng với O qua CD' nên
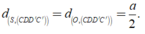
Do đó

Vậy
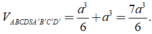

Chọn D
Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD

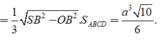
Vì H là điểm đối xứng của O qua SM nên
![]()

Vậy thể tích khối đa diện cần tính bằng
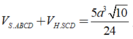

Chọn D
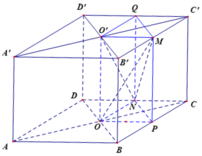
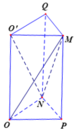
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24

Chọn đáp án D
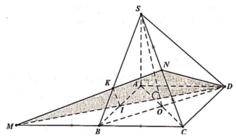
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 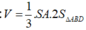
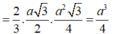
Ta có: N là trung điểm SC nên 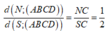
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
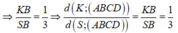
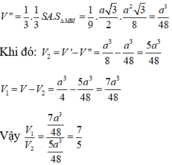

Chọn đáp án D


Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD:

FOR REVIEW |
Tam giác cân có một góc bằng 60 ° thì là tam giác đều. |

Đáp án D
S O ' O N = 1 2 OO'.ON= 1 2 . a . a 2 = a 2 4 ; M O ' = a 2 . V M O ' O N = 1 3 M O ' . S O ' O N = a 3 24 .
Chọn đáp án C.