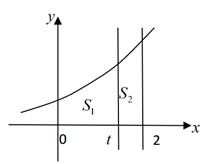
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y=0, x=0, x=2. Đường thẳng x=1 (0<t<2) chia (H) thành hai phần có diện tích S 1 và S 2 (như hình vẽ). Tìm t để S 1 = 3 S 2
A. t = log 3 5
B. t = log 3 2
C. t = log 3 35
D. t = log 3 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
S = S 1 + S 2 = ∫ 0 ln 8 e x d x = 7 Do S 1 = S 2 ⇒ S 1 = 7 2 ⇒ ∫ 0 k e x d x = 7 2 ⇔ e k - 1 = 7 2 ⇔ k = ln 9 2 .

\(S_k=\int\limits^3_k\left|2-x\right|dx=\int\limits^2_k\left(2-x\right)dx+\int\limits^3_2\left(x-2\right)dx\)
\(=\left(2x-\dfrac{x^2}{2}\right)|^2_k+\left(\dfrac{x^2}{2}-2x\right)|^3_2=\dfrac{k^2}{2}-2k+\dfrac{5}{2}=16\)
\(\Rightarrow k^2-4k-27=0\Rightarrow k=2-\sqrt{31}\)