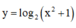Tìm đạo hàm của hàm số y = log 2 ( x 2 + 1 )
A. y ' = 2 x ( x 2 + 1 ) ln 2
B. y ' = 1 x 2 + 1
C. y ' = 1 ( x 2 + 1 ) ln 2
D. y ' = 2 x x 2 + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,y'=\left(\dfrac{1}{2x+3}\right)'=-\dfrac{2}{\left(2x+3\right)^2}\\ \Rightarrow y''=\dfrac{2\cdot\left[\left(2x+3\right)^2\right]'}{\left(2x+3\right)^4}=\dfrac{8}{\left(2x+3\right)^3}\\ b,y'=\left(log_3x\right)'=\dfrac{1}{xln3}\\ \Rightarrow y''=-\dfrac{1}{x^2ln3}\\ c,y'=\left(2^x\right)'=2^x\cdot ln2\\ \Rightarrow y''=2^x\cdot\left(ln2\right)^2\)

a) \(y' = {\left( {{x^2} - x} \right)^\prime }{.2^x} + \left( {{x^2} - x} \right).{\left( {{2^x}} \right)^\prime } = \left( {2{\rm{x}} - 1} \right){.2^x} + \left( {{x^2} - x} \right){.2^x}.\ln 2\).
b) \(y' = {\left( {{x^2}} \right)^\prime }.{\log _3}x + {x^2}.{\left( {{{\log }_3}x} \right)^\prime } = 2{\rm{x}}.{\log _3}x + {x^2}.\frac{1}{{x\ln 3}} = 2{\rm{x}}.{\log _3}x + \frac{x}{{\ln 3}}\).
c) Đặt \(u = 3{\rm{x}} + 1\) thì \(y = {e^u}\). Ta có: \(u{'_x} = {\left( {3{\rm{x}} + 1} \right)^\prime } = 3\) và \(y{'_u} = {\left( {{e^u}} \right)^\prime } = {e^u}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = {e^u}.3 = 3{{\rm{e}}^{3{\rm{x}} + 1}}\).
Vậy \(y' = 3{{\rm{e}}^{3{\rm{x}} + 1}}\).

a: \(y'=\left(sin3x\right)'+\left(sin^2x\right)'=3\cdot cos3x+sin\left(x+pi\right)\)
b: \(y'=\left(log_2\left(2x+1\right)\right)'+\left(3^{-2x+1}\right)'\)
\(=\dfrac{2}{\left(2n+1\right)\cdot ln2}-2\cdot3^{-2x+1}\cdot ln3\)

tham khảo:
a)\(y'\left(x\right)=5\left(\dfrac{2x-1}{x+2}\right)^4.\dfrac{\left(x+2\right)\left(2\right)-\left(2x-1\right).1}{\left(x+2\right)^2}\)
\(=\dfrac{10\left(2x-1\right)\left(x+2\right)^3}{\left(x+2\right)^4}=\dfrac{20x-50}{\left(x+2\right)^4}\)
b)\(y'\left(x\right)=\dfrac{2\left(x^2+1\right)-2x\left(2x\right)}{\left(x^2+1\right)^2}\)\(=\dfrac{2\left(1-x^2\right)}{\left(x^2+1\right)^2}\)
c)\(y'\left(x\right)=e^x.2sinxcosx+e^xsin^2x.2cosx\)
\(=2e^xsinx\left(cosx+sinxcosx\right)\)
\(=2e^xsinxcos^2x\)
d)\(y'\left(x\right)=\dfrac{1}{x\sqrt{x}}.\left(+\dfrac{1}{2\sqrt{x}}\right)\)
\(=\dfrac{1}{\sqrt{x}\left(2\sqrt{x}+\sqrt{x}+2\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(3\sqrt{x}+2\right)}\)

a: \(y'=\left(x^2+3x-1\right)'\cdot e^x+\left(x^2+3x-1\right)\cdot\left(e^x\right)'\)
\(=e^x\left(2x+3\right)+\left(x^2+3x-1\right)\cdot e^x\)
\(=e^x\left(x^2+5x+2\right)\)
b: \(y'=\left(x^3\right)'\cdot log_2x+x^3\cdot\left(log_2x\right)'\)
\(=3x^2\cdot log_2x+x^3\cdot\dfrac{1}{x\cdot ln2}\)

tham khảo:
a)y′=2\(^{3x-x^2}\).ln2.(3−2x)
b) y′\(\dfrac{4}{ln3}\).\(\dfrac{1}{4x+1}\).4=\(\dfrac{4}{\left(4x+1\right)ln3}\)

a, \(y=\left(2x^3+3\right)^2\)
\(y'=2\left(2x^3+3\right)6x^2\)
\(=12x^2\left(2x^3+3\right)\)
b,\(y=cos3x\)
\(y'=-3sin3x\)
c, \(y=log_2\left(x^2+2\right)\)
\(y'=\dfrac{2x}{\left(x^2+2\right)ln2}\)

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)

a,
\(y' = 6x - 4 \Rightarrow y'' = 6\)
Tại \({x_0} = - 2 \Rightarrow y''( - 2) = 6\)
b,
\(\begin{array}{l}y' = \frac{2}{{\left( {2x + 1} \right)\ln 3}}\\ \Rightarrow y'' = \left( {2.\frac{1}{{\left( {\left( {2x + 1} \right)\ln 3} \right)}}} \right)' = - 2.\frac{{\left( {\left( {2x + 1} \right)\ln 3} \right)'}}{{{{\left( {\left( {2x + 1} \right)\ln 3} \right)}^2}}}\\ = - 2\frac{{2\ln 3}}{{{{\left( {\left( {2x + 1} \right)\ln 3} \right)}^2}}} = \frac{{ - 4\ln 3}}{{{{\left( {\left( {2x + 1} \right)\ln 3} \right)}^2}}}\end{array}\)
Tại \({x_0} = 3 \Rightarrow y''(3) = \frac{{ - 4\ln 3}}{{{{\left( {\left( {2.3 + 1} \right)\ln 3} \right)}^2}}} = \frac{{ - 4\ln 3}}{{{{\left( {7\ln 3} \right)}^2}}} = \frac{{ - 4}}{{49\ln 3}}\)
c, \(y' = 4{e^{4x + 3}} \Rightarrow y'' = 16{e^{4x + 3}}\)
Tại \({x_0} = 1 \Rightarrow y''(1) = 16.{e^{4.1 + 3}} = 16.{e^7}\)
d,
\(y' = 2\cos \left( {2x + \frac{\pi }{3}} \right) \Rightarrow y'' = - 4\sin \left( {2x + \frac{\pi }{3}} \right)\)
Tại \({x_0} = \frac{\pi }{6} \Rightarrow y''\left( {\frac{\pi }{6}} \right) = - 4\sin \left( {2.\frac{\pi }{6} + \frac{\pi }{3}} \right) = - 2\sqrt 3 \)
e,
\(y' = - 3.\sin \left( {3x - \frac{\pi }{6}} \right) \Rightarrow y'' = - 9.\cos \left( {3x - \frac{\pi }{6}} \right)\)
Tại \({x_0} = 0 \Rightarrow y''(0) = - 9.\cos \left( {3.0 - \frac{\pi }{6}} \right) = \frac{{ - 9\sqrt 3 }}{2}\)
Đáp án A
Phương pháp giải: Áp dụng công thức tính đạo hàm của hàm lôgarit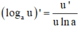
Lời giải: Ta có