Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. Chứng minh rằng đa giác AEHD và hình ABCFE có diện tích bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 7 2018
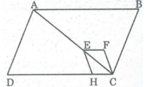
Hình ABCFE không phải là tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.
2 tháng 8 2016
nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
2 tháng 8 2016
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)
CM
27 tháng 12 2017
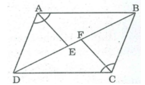
Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E
CH
Cô Hoàng Huyền
Admin
VIP
30 tháng 1 2018
Gọi O là giao điểm của AC và BD. Theo tính chất hình bình hành thì O là trung điểm AC và BD.
Gọi H, I, J, L lần lượt là chân các đường cao hạ từ D, O, C, B xuống đường thẳng xy.
Ta thấy ngay DH // OI // CJ // KB.
Xét tam giác ACJ có O là trung điểm AC, OI // CJ nên OI là đường trung bình tam giác hay CJ = 2OI. (1)
Xét hình thang vuông HDBK có O là trung điểm BD, OI // DH // BK nên OI là đường trung bình hình thang.
Vậy thì \(DH+BK=2OI\) (2)
Từ (1) và (2) suy ra CJ = DH + BK.
Suy ra \(\frac{1}{2}CJ.AE=\frac{1}{2}HD.AE+\frac{1}{2}BK.AE\) hay \(S_{ACE}=S_{ADE}+S_{ABE}\)
3 tháng 2 2018
1
Ta có do \(K\in CD;CD//AB\Rightarrow\widehat{K1}=\widehat{A2}\)
Mà \(\widehat{A2}=\widehat{A1}\)(AK LÀ PHÂN GIÁC)
\(\Rightarrow\widehat{K1}=\widehat{A1}\Rightarrow\Delta ADK\)cân tại D => AD=DK
Tương tự ta cm được BC=CK
=> AD+BC=DK+CK
Mà K nằm giữa C và D nên AD+BC=DK+CK=DC(đpcm)
YP
21 tháng 10 2021
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành
Ta có:
△ ABC = △ CDA (c.c.c) ⇒ S A B C = S C D A (1)
△ EFC = △ CHE (c.c.c) ⇒ S E F C = S C H E (2)
Từ (1) và (2) ⇒ S A B C - S E F C = S C D A - S C H E
Hay S A B C F E = S A E H D