Một sân hình tam giác có diện tích là \(180m^2\) . Tính cạnh đáy của sân, biết rằng nếu tăng cạnh đáy 4m và giảm chiều cao tương ứng 1m thì diện tích không đổi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Gọi độ dài cạnh đáy là x (cm) (x > 0)
Chiều cao của thửa ruộng có độ dài là: 360/x (cm)
Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:
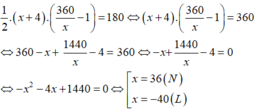
Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm

Đáp án C
Gọi độ dài cạnh đáy là x (cm) (x > 0)
Chiều cao của thửa ruộng có độ dài là: 360/x (cm)
Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:
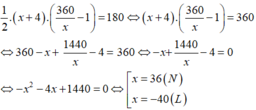
Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm

Gọi cạnh đáy của thửa ruộng là x (x > 0)
Suy ra chiều cao của thửa ruộng là 2.180 x = 360 x (m)
Vì khi tăng cạnh đáy thêm 4m và giảm chiều cao tương ứng đi 1m thì diện tích thửa ruộng không đổi nên ta có phương trình:
1 2 . 360 x − 1 x + 4 = 180 ⇔ ( 360 – x ) ( x + 4 ) = 360 x ⇔ x 2 + 4 x – 1440 = 0
⇔ x 2 – 36 x + 40 x – 1440 = 0 ⇔ x ( x – 36 ) + 40 ( x – 36 ) = 0
⇔ ( x – 36 ) ( x + 40 ) = 0 ⇔ ⇔ x = 36 ( t m d k ) x = − 40 ( k t m d k )
Vậy cạnh đáy của thửa ruộng là 36 m
Đáp án:A

Gọi chiều cao ứng với cạnh đáy của thửa ruộng là h (m); h > 4
Vì thửa ruộng hình tam giác có diện tích 120 m 2 nên chiều dài cạnh đáy thửa ruộng là 120.2/h hay 240/h (m)
Vì tăng cạnh đáy thêm 5m và chiều cao giảm đi 4m thì diện tích giảm 40 m 2 nên ta có phương trình:

Đáp án B

Bài làm :
Gọi chiều dài một cạnh cần tính là a (m) ; chiều cao tương ứng là h (m) . Điều kiện : a,h > 0
Thửa ruộng có S=2180 m2
\(\Rightarrow\frac{a.h}{2}=2180\Rightarrow a.h=4360\Rightarrow a=\frac{4360}{h}\left(1\right)\)
Tăng cạnh 4m ; giảm chiều cao tương ứng 1m thì S không đổi
\(\Rightarrow\left(a+4\right)\left(h-1\right)=4360\left(2\right)\)
Thay (1) vào (2) ; ta được :
\(\left(\frac{4360}{h}+4\right)\left(h-1\right)=4360\)
\(\Leftrightarrow\frac{\left(4360+4h\right)\left(h-1\right)}{h}=\frac{4360h}{h}\)
\(\Leftrightarrow4h^2+4356h-4360-4360h=0\)
\(\Leftrightarrow4h^2-4h-4360=0\)
\(\Delta'=2^2-4.\left(-4360\right)=17444>0\)
\(\Rightarrow\hept{\begin{cases}h_1=\frac{2+\sqrt{17444}}{4}=\frac{1+7\sqrt{89}}{2}\left(TM\right)\\h_2=\frac{2-\sqrt{17444}}{4}=\frac{1-7\sqrt{89}}{2}\left(KTM\right)\end{cases}}\)
Vậy chiều dài một cạnh cần tính là :
\(\frac{4360}{h}=\frac{4360}{\frac{1+7\sqrt{89}}{2}}=-2+14\sqrt{89}\left(m\right)\)

Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a ∈ ℕ * , dm); (a > 2)
Diện tích tam giác ban đầu là ah ( d m 2 )
Vì chiều cao bằng 1 4 cạnh đáy nên ta có phương trình h = 1 4 a
Nếu chiều cao tăng thêm 2 dm và cạnh đáy giảm đi 2 dm thì diện tích của nó tăng thêm 2,5 d m 2 .
Nên ta có phương trình 1 2 h + 2 a − 2 − 1 2 a h = 2 , 5
Ta có hệ phương trình:
h = 1 4 a 1 2 h + 2 a − 2 − 1 2 a h = 2 , 5 ⇔ h = 1 4 a − 2 h + 2 a − 4 = 5 ⇔ h = 1 4 a − 2. 1 4 a + 2 a = 9 ⇔ a = 6 h = 1 , 5 ( t m )
Vậy chiều cao và cạnh đáy của tấm bìa lần lượt là 1,5 dm và 6 dm
Đáp án: A

