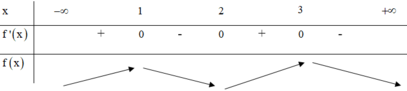
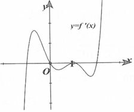
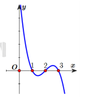
Cho hàm số y = f(x) xác định và có đạo hàm y=f'(x). Đồ thị của hàm số y = f'(x) như hình dưới đây.
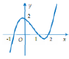
Khẳng định nào sau đây là đúng?
A. Hàm số y = f x có ba điểm cực trị.
B. Hàm số y = f x đồng biến trên khoảng − ∞ ; 2
C. Hàm số y = f x nghịch biến trên khoảng 0 ; 1
D. Hàm số y = f x đồng biến trên khoảng − ∞ ; − 1


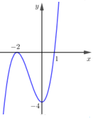
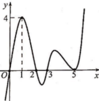
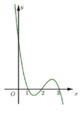


 Xét các khẳng định sau:
Xét các khẳng định sau:
Đáp án A
Phương pháp: Quan sát đồ thị hàm số y = f ' x để tìm khoảng dương, âm của f ' x , từ đó tìm được khoảng đồng biến, nghịch biến của f x .
Cách giải:
Từ đồ thị hàm số y = f ' x suy ra hàm số y = f x nghịch biến trên − ∞ − 1 và 1 ; 2 (làm y'âm) và đồng biến trên − 1 ; 1 (làm y'dương).
Suy ra B, C, D sai và A đúng.
Chú ý khi giải:
HS có thể nhầm lẫn thành đồ thị hàm số y = f x do đọc không kĩ đề dẫn đến chọn sai đáp án.