OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
24 tháng 4 2019
Đường thẳng d song song với hai mặt phẳng (P): 3x + 12y - 3z - 5 = 0, (Q): 3x - 4y + 9z = 0 và đồng thời cắt cả hai đường thẳng d 1 :   x + 5 2 = y - 3 - 4 = z + 1 3 ,  d 2 :   x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là ...
Đọc tiếp

Đường thẳng d song song với hai mặt phẳng

(P): 3x + 12y - 3z - 5 = 0,

(Q): 3x - 4y + 9z = 0 và đồng thời cắt

cả hai đường thẳng d 1 :   x + 5 2 = y - 3 - 4 = z + 1 3 ,  d 2 :   x - 3 - 2 = y + 1 3 = z - 2 4 có phương trình là

#Toán lớp 12
1
CM
Cao Minh Tâm
24 tháng 4 2019

Đáp án D

Cách giải

Vì d song song với hai mặt phẳng (P) và (Q) nên nhận

Đúng(0)
PT
Pham Trong Bach
21 tháng 8 2017
Đường thẳng d song song với hai mặt phẳng P :   3 x + 12 y - 3 z - 5 = 0 ,   Q :   3 x - 4 y + 9 z + 7 = 0  và đồng thời cắt cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 ,   d 2 :   x - 3 - ...
Đọc tiếp

Đường thẳng d song song với hai mặt phẳng P :   3 x + 12 y - 3 z - 5 = 0 ,   Q :   3 x - 4 y + 9 z + 7 = 0  và đồng thời cắt cả hai đường thẳng d 1 : x + 5 2 = y - 3 - 4 = z + 1 3 ,   d 2 :   x - 3 - 2 = y + 1 3 = z - 2 4  có phương trình là

A.  x + 3 8 = y + 1 3 = z - 2 4

B. x - 3 8 = y + 1 3 = z - 2 4

C. x + 3 - 8 = y + 1 3 = z + 2 4

D. x + 3 - 8 = y + 1 3 = z - 2 4

#Mẫu giáo
1
CM
Cao Minh Tâm
21 tháng 8 2017

Chọn D

Cách giải : Vì d song song với hai mặt phẳng (P) và (Q) nên nhận    

Đúng(0)
PT
Pham Trong Bach
22 tháng 10 2018
Trong không gian Oxyz viết phương trình đường thẳng d song song với hai mặt phẳng (P): 3x+12y-3z-5=0, (Q): 3x-4y+9z+7=0 và đồng thời cắt cả hai đường thẳng d 1 :   x + 5 2 = y - 3 - 4 = z + 1 3 , d 2 :   x - 3 - 2 = y + 1 3 = z - 2 ...
Đọc tiếp

Trong không gian Oxyz viết phương trình đường thẳng d song song với hai mặt phẳng (P): 3x+12y-3z-5=0, (Q): 3x-4y+9z+7=0 và đồng thời cắt cả hai đường thẳng d 1 :   x + 5 2 = y - 3 - 4 = z + 1 3 ,

d 2 :   x - 3 - 2 = y + 1 3 = z - 2 4

A.  x + 3 8 = y + 1 3 = z - 2 4

B.  x - 3 8 = y + 1 3 = z - 2 4

C.  x + 3 - 8 = y + 1 3 = z + 2 4

D.  x + 3 - 8 = y + 1 3 = z - 2 4

#Mẫu giáo
1
CM
Cao Minh Tâm
22 tháng 10 2018

Đúng(0)
PT
Pham Trong Bach
28 tháng 7 2018
Trong không gian Oxyz, cho điểm A(1;1;-2) và hai mặt phẳng (P): 3x - y +1 = 0, (Q): x - 2z - 3 = 0. Phương trình đường thẳng d qua điểm A đồng thời song song với cả hai mặt phẳng (P), (Q) là A.  x = 2 + t y = − 6 + t z = 1 − 2 t . B.  x = 5 + 2 t y = 13 + 6 ...
Đọc tiếp

Trong không gian Oxyz, cho điểm A(1;1;-2) và hai mặt phẳng (P): 3x - y +1 = 0, (Q): x - 2z - 3 = 0. Phương trình đường thẳng d qua điểm A đồng thời song song với cả hai mặt phẳng (P), (Q) là

A.  x = 2 + t y = − 6 + t z = 1 − 2 t .

B.  x = 5 + 2 t y = 13 + 6 t z = t .

C.  x = 1 + 2 t y = 1 − 6 t z = − 2 + t .

D.  x = 2 + t y = 6 + t z = 1 − 2 t .

#Mẫu giáo
1
CM
Cao Minh Tâm
28 tháng 7 2018

Đáp án B

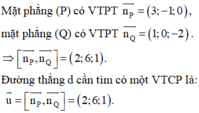
Vì  A 1 ; 1 ; − 2 ∈ d  nên phương trình của đường thẳng d là: x = 1 + 2 t y = 1 + 6 t z = − 2 + t

Đúng(0)
PT
Pham Trong Bach
6 tháng 8 2019
Trong không gian Oxyz, cho hai mặt phẳng ( P ) :   3 x - y - 3 z + 2 = 0  và ( Q ) :   - 4 x + y + 2 z + 1 = 0  Phương trình đường thẳng đi qua gốc tọa độ O và song song với 2 đường thẳng (P) và (Q) là: ...
Đọc tiếp

Trong không gian Oxyz, cho hai mặt phẳng ( P ) :   3 x - y - 3 z + 2 = 0  và ( Q ) :   - 4 x + y + 2 z + 1 = 0  Phương trình đường thẳng đi qua gốc tọa độ O và song song với 2 đường thẳng (P) và (Q) là:
#Toán lớp 12
1
CM
Cao Minh Tâm
6 tháng 8 2019

Đáp án D.

Đường thẳng đó có véc tơ chỉ phương:

Đúng(0)
PT
Pham Trong Bach
15 tháng 6 2017
Trong không gian Oxyz, cho hai mặt phẳng P : 3 x − y − 3 z + 2 = 0  và Q : − 4 x + y + 2 z + 1 = 0.  Phương trình đường thẳng đi qua gốc tọa độ O và song song với 2 đường thẳng (P) và (Q) là: A.  x 1 = y − 1 = z 6 . B.  x 1 = y − 6 = z − ...
Đọc tiếp

Trong không gian Oxyz, cho hai mặt phẳng P : 3 x − y − 3 z + 2 = 0  và Q : − 4 x + y + 2 z + 1 = 0.  Phương trình đường thẳng đi qua gốc tọa độ O và song song với 2 đường thẳng (P) và (Q) là:

A.  x 1 = y − 1 = z 6 .

B.  x 1 = y − 6 = z − 1 .

C.  x 1 = y 1 = z 6 .

D.  x 1 = y 6 = z − 1 .

#Mẫu giáo
1
CM
Cao Minh Tâm
15 tháng 6 2017

Đáp án D.

Đường thẳng đó có véc tơ chỉ phương:

u → = n 1 → ; n 2 → = 3 ; − 1 ; − 3 ; − 4 ; 1 ; 2 = 1 ; 6 ; − 1 .

 

Đúng(0)
DT
Đỗ Thành Công
24 tháng 7 2021

Cho đường thẳng (d): 3x−4y+5=03x-4y+5=0. Viết phương trình đường thẳng đi qua điểm M(2;1) và song song với đường thẳng d?

 A. −3x−4y−2=0-3x-4y-2=0

 B. Đáp án khác

 C. 3x+4y−2=03x+4y-2=0

 D. 3x−4y−2=0
#Toán lớp 10
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2021

Đường thẳng song song d nên nhận (3;-4) là 1 vtpt

Phương trình:

\(3\left(x-2\right)-4\left(y-1\right)=0\Leftrightarrow3x-4y-2=0\)

Đúng(0)
PM
Phí Minh Hạnh
4 tháng 5 2023
Trong mặt phẳng tọa độ Oxy cho m điểm M 1,0 và đường thẳng  d :x -4y +5=0. a ,viết phương trình đường thẳng d qua m và song song với đường thẳng d x - 4y + 5 = 0  b,viết phương trình đường thẳng d qua m và vuông góc với đường thẳng d x - 4y + 5 = 0 , C,Viết phương trình đường tròn {C}  M  và tiếp xúc với đường thẳng d x - 4y + 5 =...
Đọc tiếp

Trong mặt phẳng tọa độ Oxy cho m điểm M 1,0 và đường thẳng  d :x -4y +5=0. a ,viết phương trình đường thẳng d qua m và song song với đường thẳng d x - 4y + 5 = 0  b,viết phương trình đường thẳng d qua m và vuông góc với đường thẳng d x - 4y + 5 = 0 , C,Viết phương trình đường tròn {C}  M  và tiếp xúc với đường thẳng d x - 4y + 5 = 0
#Toán lớp 10
1
NL
Nguyễn Lê Phước Thịnh
11 tháng 5 2023

a: Vì (d)//x-4y+5=0 nên (d): x-4y+c=0

Thay x=1 và y=0 vào (d), ta được:

c+1=0

=>c=-1

=>x-4y-1=0

b: Vì (d) vuông góc x-4y+5=0

nên (d): 4x+y+c=0

Thay x=1 và y=0 vào (d), ta được:

c+4=0

=>c=-4

=>4x+y-4=0

Đúng(1)
PT
Pham Trong Bach
11 tháng 4 2019
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và hai mặt phẳng P :   2 x + 3 y = 0 ,   Q :   3 x + 4 y = 0 . Đường thẳng qua A song song với hai mặt phẳng P ,   Q có phương trình tham số là  A.  x = 1 + t y = 2 + t z = ...
Đọc tiếp

Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và hai mặt phẳng P :   2 x + 3 y = 0 ,   Q :   3 x + 4 y = 0 . Đường thẳng qua A song song với hai mặt phẳng P ,   Q có phương trình tham số là 

A.  x = 1 + t y = 2 + t z = 3 + t

B. x = 1 y = 2 z = t

C. x = t y = 2 z = 3 + t

D. x = 1 y = t z = 3

#Mẫu giáo
1
CM
Cao Minh Tâm
11 tháng 4 2019

Chọn đáp án B

Đúng(0)
PT
Pham Trong Bach
2 tháng 1 2017
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P); (Q) có phương trình tham số là: A.  x = t y = 2 z = 3 + t B.  x = 1 y = 1 z = 3 C.  x = 1 + t ...
Đọc tiếp

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và hai mặt phẳng (P): 2x+3y=0 và (Q): 3x+4y=0. Đường thẳng qua A song song với hai mặt phẳng (P); (Q) có phương trình tham số là:

A.  x = t y = 2 z = 3 + t

B.  x = 1 y = 1 z = 3

C.  x = 1 + t y = 2 + t z = 3 + t

D.  x = 1 y = 2 z = t

#Mẫu giáo
1
CM
Cao Minh Tâm
2 tháng 1 2017

Đáp án D

Phương pháp :

Đường thẳng qua A song song với hai mặt phẳng (P); (Q) nhận là 1VTCP.

Cách giải : Ta có  lần lượt là các VTPT của

Ta có :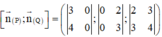 

 là 1 VTCP của đường thẳng qua A và vuông góc với cả

Vậy phương trình đường thẳng cần tìm là: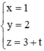 

Với t = -3  ta có đường thẳng đi qua điểm B(1;2;0) => phương trình đường thẳng cần tìm là : 

x = 1 y = 2 z = t

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP