Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

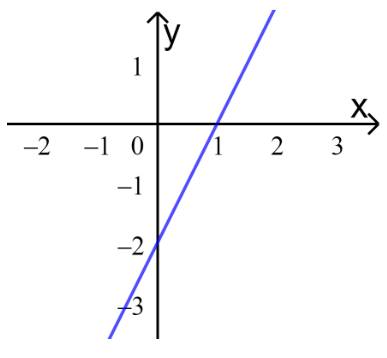
a) Cho \(x=0\Rightarrow y=-2\)
Cho \(y=0\Rightarrow x=1\)
Nối hai điểm (0;-2) và (1;0) ta được:
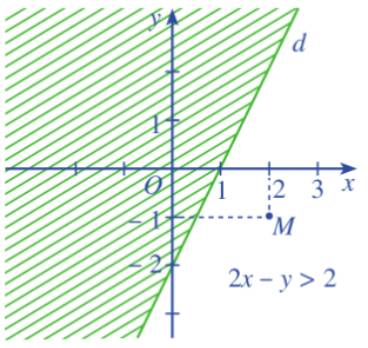
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
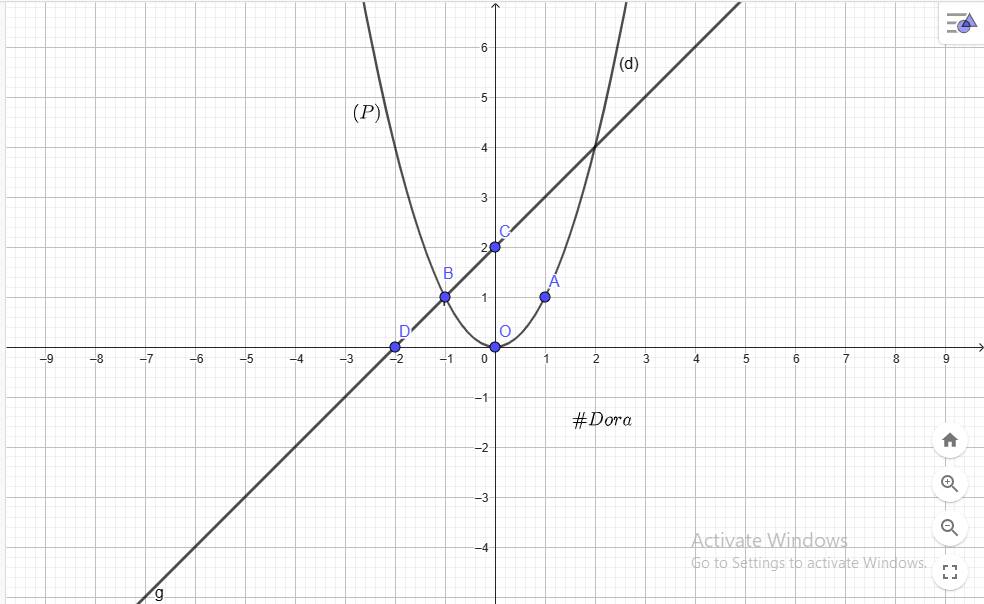
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

Bài 2:
a: \(R=d\left(I;d\right)=\dfrac{\left|-2\cdot3+1\cdot\left(-4\right)\right|}{\sqrt{3^2+\left(-4\right)^2}}=2\)
Phương trình (C) là:
(x+2)^2+(y-1)^2=2^2=4
Bài 1:
a: I thuộc Δ nên I(x;-2x-3)
IA=IB
=>IA^2=IB^2
=>\(\left(x+5\right)^2+\left(-2x-3-1\right)^2=\left(x+2\right)^2+\left(-2x-3-4\right)^2\)
=>x^2+10x+25+4x^2+16x+16=x^2+4x+4+4x^2+28x+49
=>26x+41=32x+53
=>-6x=-12
=>x=2
=>I(2;-7): R=IA=căn 113
Phương trình (C) là:
(x-2)^2+(y+7)^2=113
2: vecto IA=(7;-8)
Phương trình tiếp tuyến là:
7(x+5)+(-8)(y-1)=0
=>7x+35-8y+8=0
=>7x-8y+43=0

Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

a) Gọi đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=a'x+b'\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow a'=2\)
Vậy phương trình đường thẳng (d') có dạng \(\left(d'\right):y=2x+b'\)
Mặt khác (d') đi qua M(3;4) nên điểm M(3;4) thuộc \(\left(d'\right):y=2x+b'\)
Thay \(x=3;y=4\)vào hàm số \(y=2x+b'\)ta có:
\(4=2.3+b'\Leftrightarrow b'=-2\)
Vậy phương trình đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=2x-2\)
b) Gọi OH là khoảng cách từ O đến (d). Gọi giao điểm của (d):y = 2x + 6 với hai trục Ox, Oy lần lượt là A(xA;0), B(0;yB).
Thay x = xA; y = 0 vào hàm số y = 2x + 6, ta có: \(0=2x_A+6\Leftrightarrow x_A=-3\)
Thay x = 0; y = yB vào hàm số y = 2x + 6, ta có: \(y_B=2.0+6=6\)
Vì \(OA=\left|x_A\right|;OB=\left|y_B\right|\)\(\Rightarrow OA=\left|-3\right|=3;OB=\left|6\right|=6\)
\(\Delta OAB\)vuông tại O, đường cao OH \(\Rightarrow\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\left(htl\right)\)
Rồi bạn thay OA, OB vào và dễ dàng tính được OH