Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Đặt z = a+ bi.
Theo đề ra ta có: ( 3 + i) z = 2
Hay ( 3 + i)( a + bi) = 2
Suy ra: 3a - b + ( 3b + a) i = 2
nên z = 3/5 - 1/5i.
Khi đó w = 3/5 - 1/5i + 2/5 - 4/5 i = 1 - i.
Vậy 
Gọi z = a + bi với a , b ∈ ℝ
Khi đó phương trình z + z 1 + i + z - z 2 + 3 i = 4 - i trở thành:
2 a 1 + i + 2 b 2 + 3 i = 4 - i ⇔ 2 a + 4 b + 2 a + 6 b i = 4 - i
Do đó:
2 a + 4 b = 4 2 a + 6 b = - 1 a = 1 2 b = - 1 2 ⇒ z = 1 2 - 1 2 i
Ta có: w = z 3 + z + 1 z 2 + 1 - = z + 1 z 2 + 1 Thay 1 2 - 1 2 i vào ta được:
w = 1 2 - 1 2 i + 1 1 2 - 1 2 i 2 + 1 = 1 2 - 1 2 i + 1 - 1 2 i + 1 = 13 10 - 1 10 i
Suy ra w = 13 10 2 + - 1 10 2 = 170 10
Đáp án A
Chọn C.
Áp dụng công thức: 
Ta có: 
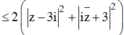
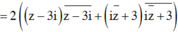
Giải bất phương trình 100 ≤ 4 ta có 
ta có 0 ≤ |z| ≤ 4
Vậy min|z| = 4 đạt được khi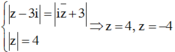 
gọi z= a + bi \(\left(a,b\in R\right)\)
(2+i)(a+bi)=4-3i
\(\Leftrightarrow\) \(2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
w= i(1-2i) + 2( 1+ 2i) = 4 + 5i
Gọi \(z=a+bi\left(a,b\in R\right)\)
\(\left(2+i\right)\left(a+bi=4-3i\right)\)
\(\Leftrightarrow2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
\(w=i\left(1-2i\right)+2\left(1+2i\right)=4+5i\)
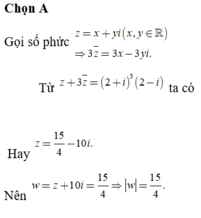
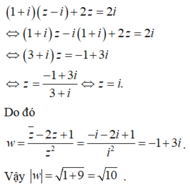
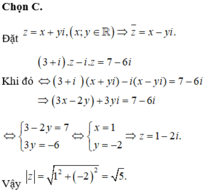
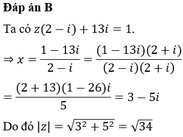
Đáp án A.