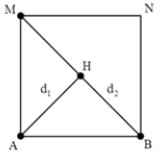
Hai nguồn sóng kết hợp A, B trên mặt thoáng chất lỏng dao động theo phương trình u A = u B = 4 cos ( 10 π t ) m m . Coi biên độ sóng không đổi, tốc độ sóng v = 15cm/s. Hai điểm M 1 , M 2 cùng nằm trên một elip nhận A, B làm tiêu điểm có A M 1 - B M 1 = 1 c m và A M 2 - B M 2 = 3 , 5 c m . Tại thời điểm li độ của M1 là 3mm thì li độ của M2 tại thời điểm đó là
A. −3mm.
B. −3mm.
C. 3mm.
D. −33mm.

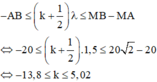
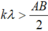
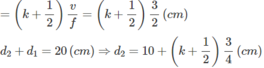
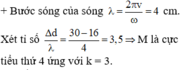
Đáp án D
Ta có bước sóng λ = v f = 3(cm)
Mọi điểm nằm trên Elip có tiêu điểm là A và B đều có cùng pha dao động.