Các góc tương ướng bằng nhau là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 5 2019
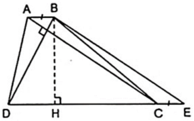
Xét hình thang ABCD ( AB//CD ) có AC ⊥ BD và AC = 6dm, BD = 3,6dm.
Kẻ đường cao BH của hình thang.
Ta có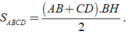
Kẻ BE//AC thì BD ⊥ BE thì hình thang ABEC có hai cặp cạnh đối song song → ABEC là hình bình hành.
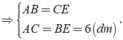
Do đó, ta có: CD + AB = CD + CE = DE
Khi đó ta có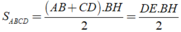
⇒ S là diện tích của tam giác DBE vuông tại B.
Khi đó S = 1 2 B D . B E = 1 2 . 3 , 6 . 6 = 10 , 8 ( d m 2 )
Vậy diện tích của hình thang là 10 , 8 ( d m 2 )
19 tháng 5 2019
ko chép lại đề
= góc P
= góc Q
= góc R
=cạnh PQ
= cạnh PR
= cạnh QR
30 tháng 6 2015
Tích của chiều cao với cạnh đáy là :
64 x 2 = 128 (m)
Vậy chiều cao của hình tam giác đó là :
128 : 8 = 16 (m)
23 tháng 4 2020
CÂu 1 : D) 2 cạnh tương ứng bằng nhau 2 góc tương ứng bằng nhau
TT
23 tháng 4 2020
Câu 1. Hai tam giác gọi là bằng nhau nếu có:
A. Các cạnh tương ứng bằng nhau.
B. Các góc tương ứng bằng nhau.
C. Các cạnh bằng nhau và các góc bằng nhau.
D.Các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
Câu 2.Cho tam giác ABC vuông cân tại A thì:
A. BC=AC+AB B. AB^2=BC^2+AC^2
C. BC^2=AC^2+AB^2 D. AB=BC+AC
Hok tốt!!!
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Quan sát hình vẽ ta thấy:
- Các cạnh tương ứng bằng nhau.
- Các góc tương ứng bằng nhau.
21 tháng 10 2016
a) Cạnh tương ứng với cạnh BC là IK
Góc tương ứng với góc H là góc A
b) Các cạnh bằng nhau: AB và HI; AC và HK; BC và IK
Các góc bằng nhau: góc A và góc H; góc B và góc I; góc C và góc K