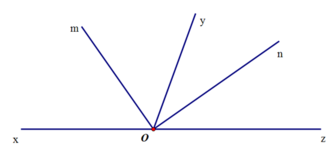
Cho hai góc kề bù x O y ^ và z O y ^ sao cho z O y ^ = 70 0 a) Tính số đo x...

PT

Pham Trong Bach

26 tháng 4 2019

Cho hai góc kề bù x O y ^ và z O y ^ sao cho z O y ^ = 70 0 a) Tính số đo x O y ^ ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

1

CM

Cao Minh Tâm

26 tháng 4 2019

Đúng(0)

NN

nguyen nhu quynh huong

21 tháng 4 2018 - olm

Cho góc xOz kề bù góc y o z biết rằng góc x O y- góc y o z = 20 độ Tính góc xOy và góc yOz

#Hỏi cộng đồng OLM #Toán lớp 6

0

BN

Bùi Nguyễn Hà Linh

21 tháng 4 2020 - olm

Cho Oy, OxOy,Ox lần lượt là tia phân giác của hai góc kề bù \widehat{nOm},\widehat{mOz}nOm,mOz. Tính số đo góc \widehat{yOx}yOx.

#Hỏi cộng đồng OLM #Toán lớp 6

1

BN

Bùi Nguyễn Hà Linh

21 tháng 4 2020

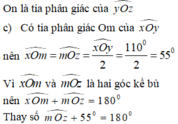
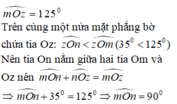
Theo đề bài, ta có \widehat{nOz}=\frac{1}{2}\widehat{xOz},\widehat{mOz}=\frac{1}{2}\widehat{zOy}nOz=21xOz,mOz=21zOy.

Mặt khác, \widehat{xOz},\widehat{zOy}xOz,zOy là hai góc kề bù nên \widehat{xOz}+\widehat{zOy}=180^o.xOz+zOy=180o.

Do đó \widehat{nOm}=\widehat{nOz}+\widehat{mOz}=\frac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=90^onOm=nOz+mOz=21(xOz+yOz)=90o.

Đúng(0)

LA

Lan Anh

24 tháng 4 2018 - olm

1)Cho góc xOy có số đo bằng 90 độ .vẽ tia oz nằm giữa hai tia Ox và Oy sao cho góc x o t = 30 độ

A) tính số đo góc yOt

B) hỏi đi ô tô có phải là tia phân giác của góc x O y k ?vì sao?

2) Cho hai góc kề bù x O y và yox', biết góc xOy = góc yOx'. Chứng tỏ góc xOy là góc vuông.

#Hỏi cộng đồng OLM #Toán lớp 6

1

HH

hoàng hà phương ánh

24 tháng 4 2018

a)góc yot =60 độ b)ko,vì xot và yot ko = nhau

Đúng(0)

TM

Trương Mỹ Hoa

25 tháng 10 2023

1) Vẽ hai đường thẳng x x' & y y' cắt nhau tại O.
a) Viết tên các cặp góc đối đỉnh
b) Viết tên các cặp góc bù nhau
2) Vẽ góc xoy=30^o. Vẽ góc yoy kề bù với góc xoy ; vẽ góc yox đối đỉnh góc xoy
a) Tính số đo góc yoy
b) Tính số đo góc xox

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 10 2023

1:

a: Hai cặp góc đối đỉnh là \(\widehat{xOy};\widehat{x'Oy'}\) và \(\widehat{xOy'};\widehat{x'Oy}\)

b: hai cặp góc bù nhau là:

\(\widehat{xOy};\widehat{xOy'}\)

\(\widehat{x'Oy};\widehat{x'Oy'}\)

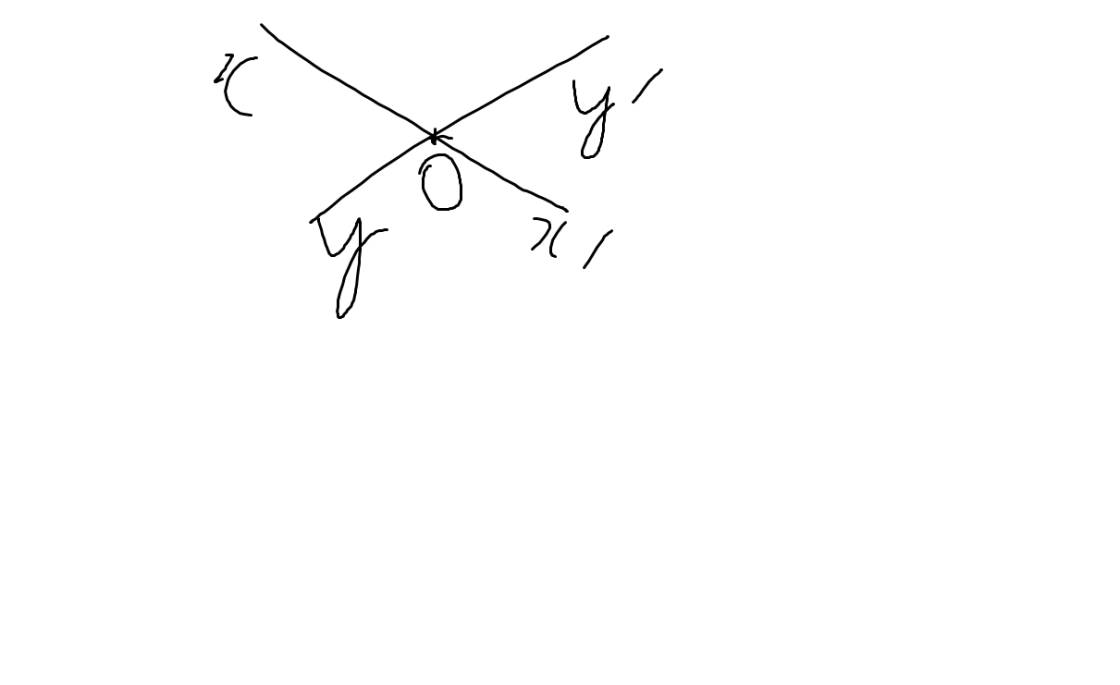
loading...

Đúng(0)

SL

Sarah Lalle y

16 tháng 2 2017 - olm

Trên đường thẳng xy , lấy điểm O . Trên cùng nửa mặt phẳng bờ là đường thẳng xy vẽ 2 tia Om và On sao cho hai góc \(x\widehat{O}m\) và \(y\widehat{O}n\) là hai góc phụ nhau và \(x\widehat{O}m\) = \(56^0\) a ) Tính góc \(y\widehat{O}n\)b ) Tính góc kề bù với góc \(x\widehat{O}m\)c ) Tính góc kề bù với góc \(y\widehat{O}n\)Giúp mk với nha các...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

1

LA

Lê Anh Tú

16 tháng 2 2017

khó quá bạn ạ

Đúng(0)

TD

Tran Duc Dung

25 tháng 4 2015 - olm

Trên cùng một nửa mặt phẳng bờ chứa điểm O , vẽ hai tia Oz và Ot sao cho xoz =45 độ yOt = 70 độ ?

Tính số đo góc kề bù zOx

Tính số đo góc tOz

#Hỏi cộng đồng OLM #Toán lớp 6

1

NH

nguyễn hồng trang

25 tháng 4 2015

góc kề bù có số đo 180độ

xoz cộng zox=yot

45 cộng zox=70

zox=70_45=24=25

Đúng(0)

NK

nguyễn khánh ngọc linh

18 tháng 4 2018 - olm

x*(x+2)=0
chiều dài hình chữ nhật = 120% chiều rộng .Biết chiều dài hơn chiều rộng 1.6 cm .Tính chu vi và S hình chữ nhật
trên cùng 1 nửa mp bờ xy chứa điểm O, xác định hai tia ou và ov sao cho góc xou=45 độ ,góc yov=70 độ .Tính số đo góc kề bù vs góc uox .Tính số đo góc uov
50%*x+2/3*x=x+4

#Hỏi cộng đồng OLM #Toán lớp 6

2

TC

Trần Cao Vỹ Lượng

18 tháng 4 2018

1 \(x\cdot\left(x+2\right)=0\Rightarrow x=0\)

4. \(50\%\cdot x+\frac{2}{3}\cdot x=x+4\Rightarrow x=24\)

Đúng(0)

NK

nguyễn khánh ngọc linh

2 tháng 5 2018

25%*x+0.5*x+x/3=-26
giải rõ ra hộ mk nha .

Đúng(0)

TT

tran thi phuong linh

24 tháng 7 2017 - olm

Cho tia Om là phân giác của góc xOy phẩy n là tia phân giác của góc đối đỉnh của góc góc xOy

a.Biết x O y = 50 độ chấm Hãy tính số đo của hai góc kề bù với góc xOy.

b. Các tia phân giác của Ok và Ohcủa các góc kề bù để có phải là hai tia đối nhau không?Tại sao?

#Hỏi cộng đồng OLM #Toán lớp 7

0

ML

manh lam

1 tháng 9 2021

cho 2 góc kề bù x o m và m o y, biết x o m=40

#Hỏi cộng đồng OLM #Toán lớp 6

4

K

Kậu...chủ...nhỏ...!!!

1 tháng 9 2021

đề thiếu

Đúng(2)

ML

manh lam

1 tháng 9 2021

thếu j

Đúng(0)

RD

Rowlie dayy

2 tháng 11 2023 - olm

cho 2 đường thẳng xx' và yy' cắt nhau tại O sao cho góc xOy bằng 70 độ a) kể tên các cặp góc kề bù và đối đỉnh có trong hình b) tính số đo góc xOy'

#Hỏi cộng đồng OLM #Toán lớp 7

1

P

Phong

CTVHS

2 tháng 11 2023

a) Các cặp góc kề bù

\(\widehat{xOy}\) và \(\widehat{yOx'}\)

\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)

\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)

\(\widehat{xOy'}\) và \(\widehat{xOy}\)

Các cặp góc đối:

\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)

\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)

b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)

\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)

\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP