Trên nửa mặt phẳng bờ chứa tia Ox vẽ x O t ^ = 40 ° , x O y ^ = 80 °
a) Tia nào nằm giữa hai tia còn lại ? Vì sao ?
b) Tính y O t ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\frac{x}{4}=\frac{4}{x^3}\Rightarrow x.x^3=4.4\Rightarrow x^4=16\Rightarrow x=\orbr{\begin{cases}-2\\2\end{cases}}\)
Vậy x = 2 hoặc x = -2
2)
a) Vì: \(\widehat{xOz}< \widehat{xOt}\left(40^0< 90^0\right)\)
=> Tia Oz nằm giữa hai tia Ox và Ot
b) Ta có: \(\widehat{xOz}+\widehat{xOm}=40^0+140^0=180^0\)
=> Hai góc này kề bù với nhau
=> Oz và Om là hai tia đối nhau
a, \(x.x^3=4.4\)
\(x^4=16\)
\(x^4=\left(\pm2\right)^4\)
=>x = \(\pm\)2

Trả lời
a)Vì trên cùng 1 nửa mặt phẳng có bờ là tia Ox ta có:
\(\widehat{xoy}\)\(=40^0< \widehat{xOz}\)\(=80^0\)
\(\Rightarrow\)Tia Oy nằm giữa 2 tia Oz và Ox
Vậy tia Oy nằm giữa 2 tia Oz và Ox
b) Từ ý (a) => Tia Oy nằm giữa 2 tia Oz là Ox
=> \(\widehat{yOz}\)\(=\widehat{xOz}\)\(-\widehat{xOy}\)
\(\Rightarrow\widehat{yOz}\)\(=80^0-40^0\)
\(\Rightarrow\widehat{yOz}\)\(=40^0\)
\(\Rightarrow\widehat{yOz}\)\(=\widehat{zOy}\)\(=\widehat{\frac{xoy}{2}}\)
=> Tia Oy là tia phân giác của \(\widehat{xOz}\)
Vậy tia Oy là tia phân giác của \(\widehat{xOz}\)
Vì trên cùng 1 nửa mặt phẳng có bờ chứa ox , xoz.xoy suy ra oy nằm giữa 2 tia ox và oz
b,Vì oy nằm giữa ox và oz suy ra xoy +yoz=xoz
thay số: 40+yoz=80
yoz=80-40
yoz=40
Vì 40=40 suy ra xoy=yoz ,oy nằm giữa ox và oz suy ra oy là tia phân giác của xoy

a/ oy nằm giữa vì xoz > xoy
b/ vì oy nằm giữa nên ta có hệ thức : yoz + yox = xoz
=> yoz = xoz - xoy
= 80 - 40 = 40 độ
c/ vì zoy + yox = xor ( chứng minh được oy nằm giữa)
vì xoy = yoz = 40 độ ( chứng minh được oy cách điều oz , ox)

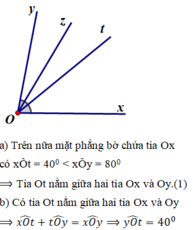
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOt}\left(40^0< 80^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Ot
b) Ta có:tia Oy nằm giữa hai tia Ox và Ot(cmt)
nên \(\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
\(\Leftrightarrow\widehat{yOt}+40^0=80^0\)
hay \(\widehat{yOt}=40^0\)
Ta có: tia Oy nằm giữa hai tia Ox và Ot(cmt)
mà \(\widehat{xOy}=\widehat{yOt}\left(=40^0\right)\)
nên Oy là tia phân giác của \(\widehat{xOt}\)