Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có bảng biến thiên như sau
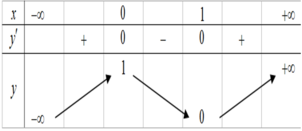
Khi đó f x = m có bốn nghiệm phân biệt x 1 < x 2 < x 3 < 1 / 2 < x 4 khi và chỉ khi
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có f ( 0 ) = 0 f ( 1 ) = 0 f ' ( 0 ) = 0 f ' ( 1 ) = 0
↔ a = 2 b = - 3 c = 0 d = 1
, suy ra hàm số đã cho là : y= 2x3-3x2+ 1.
Ta thấy: f(x) = 0 ↔ x = 0 hoặc x = -1/2
Bảng biến thiên của hàm số y = |f(x)| như sau:
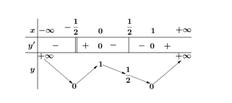
Dựa vào bảng biến thiên suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x1< x2< x3< ½< x4 khi và chỉ khi ½< m< 1.
Chọn A.

Đáp án D
Hàm số f(x) có dạng f ( x ) = ( x + 2 ) ( x - 1 ) 2 Giao với trục Oy tại (0, 2) .
=> 2<m<4.
Chọn phương án D.
Đáp án B
Ta có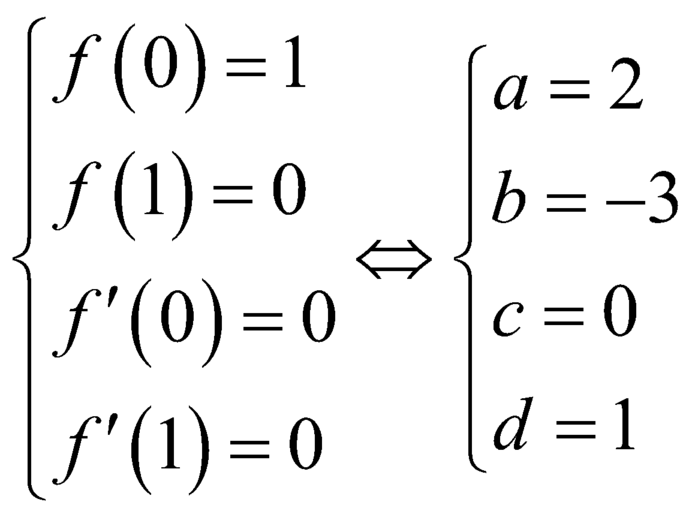
suy ra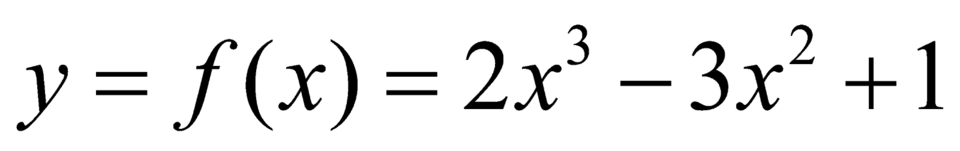 .
.
Ta có: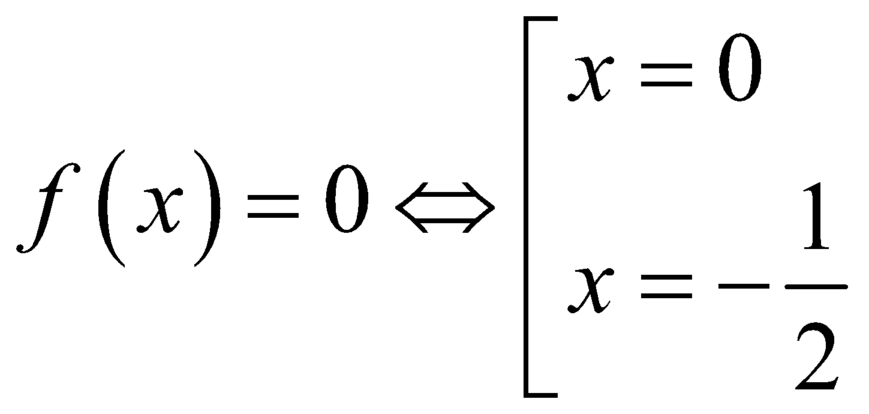 .
.
Bảng biến thiên của hàm số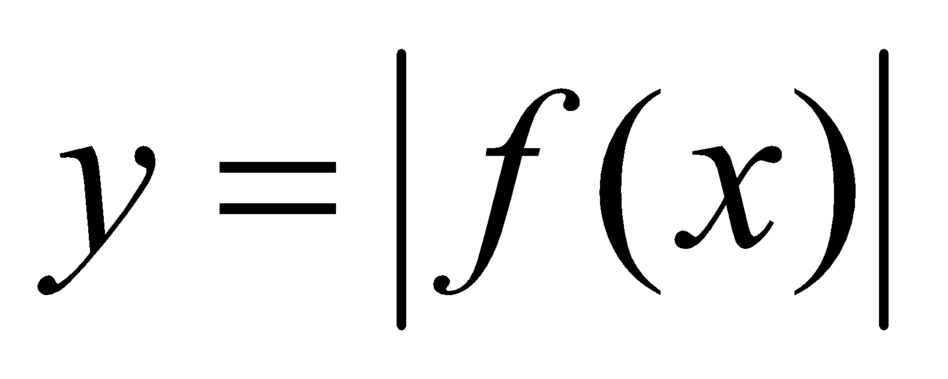 như sau:
như sau:
Dựa vào bảng biến thiên suy ra phương trình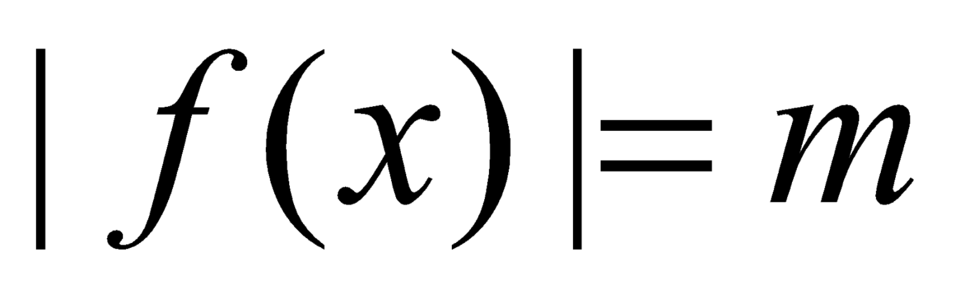 có bốn nghiệm phân biệt
có bốn nghiệm phân biệt 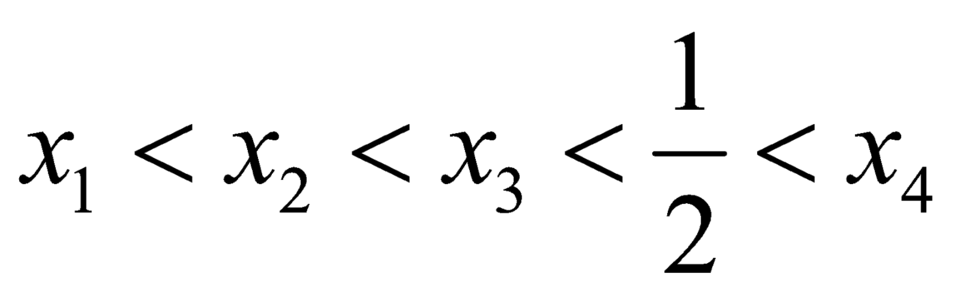 khi và chỉ khi
khi và chỉ khi 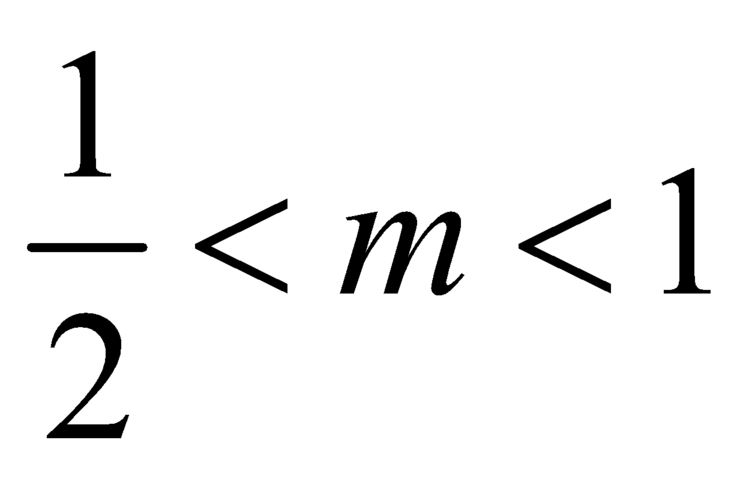 .
.