Hiện nay urani tự nhiên chứa hai đồng vị phóng xa U 235 và U 238 , với tỉ lệ số hạt U 235 và số hạt U 238 là 7/1000. Biết chu kỳ bán rã của U 235 và U 238 lần lượt là 7 , 00 . 10 8 năm và 4 , 50 . 10 9 năm. Cách đây bao nhiêu năm, urani tự nhiên có tỷ lệ số hạt U 235 và số hat U 238 là 3/100?
A. 2,74 tỉ năm
B. 1,74 tỉ năm
C. 2,22 tỉ năm
D. 3,15 tỉ năm


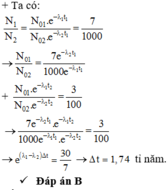
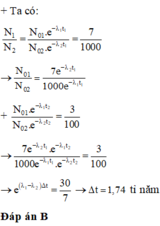
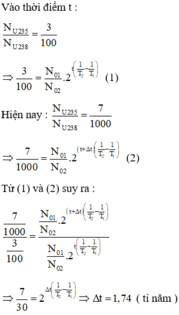
Chọn đáp án B