Trong số các số bên phải của các đa thức sau, số nào là nghiệm của đa thức bên trái nó?
Q x = x 2 + x ; - 1 0 1 2 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M(x) = x2 – 3x + 2
M(-2) = (-2)2 – 3.(-2) + 2 = 4 + 6 + 2 = 12 ≠ 0
M(-1) = (-1)2 – 3.(-1) + 2 = 1 + 3 + 2 = 6 ≠ 0
M(1) = 12 – 3.1 + 2 = 1 – 3 + 2 = 0
M(2) = 22 – 3.2 + 2 = 4 – 6 + 2 = 0
Vậy x = 1 và x = 2 là nghiệm của M(x).

A(x) = 2x – 6
A(-3) = 2.(-3) – 6 = – 6 – 6 = –12 ≠ 0
A(0) = 2.0– 6 = 0 – 6 = – 6 ≠ 0
A(3) = 2.3 – 6 = 6 – 6 = 0
Vậy x = 3 là nghiệm của A(x).

P(x) = x2 + 5x – 6
P(-6) = (-6)2 + 5.(-6) – 6 = 36 – 30 – 6 = 0
P(-1) = (-1)2 + 5.(-1) – 6 = 1 - 5 – 6 = - 10 ≠ 0
P(1) = 12 + 5.1 – 6 = 1 + 5 – 6 = 0
P(6) = 62 + 5.6 – 6 = 36 + 30 – 6 = 60 ≠ 0
Vậy -6 và 1 là nghiệm của P(x).

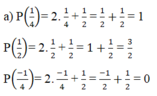
Vậy x = 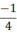 là nghiệm của đa thức P(x) = 2x +
là nghiệm của đa thức P(x) = 2x + 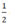
b) Q(3) = 32 – 2.3 – 3 = 9 – 6 – 3 = 0
Q(1) = 12 – 2.1 – 3 = 1 – 2 – 3 = - 4
Q(-1) = (-1)2 – 2.(-1) – 3 = 1 + 2 – 3 = 0
Vậy x = 3 và x = - 1 là nghiệm của đa thức Q(x) = x2 – 2x – 3

a) Ta có: P(\( - \dfrac{1}{8}\)) = 4.(\( - \dfrac{1}{8}\))+ \(\dfrac{1}{2}\)= (-\(\dfrac{1}{2}\)) + \(\dfrac{1}{2}\) = 0
Vậy \(x = - \dfrac{1}{8}\) là nghiệm của đa thức P(x) = 4x + \(\dfrac{1}{2}\)
b) Q(1) = 12 +1 – 2 = 0
Q(-1) = (-1)2 + (-1) – 2 = -2
Q(2) = 22 + 2 – 2 = 4
Vì Q(1) = 0 nên x = 1 là nghiệm của Q(x)
Q(x) = x2 + x
Q(-1) = (-1)2 + (-1) = 1 – 1 = 0
Q(0) = 02 + 0 = 0 + 0 = 0
Q(1) = 12 + 1 = 1 + 1 = 2 ≠ 0.
Vậy -1 và 0 là nghiệm của Q(x).