Cho hình chóp S.ABC có AC = a, AB = a 3 , B A C ^ = 150 ∘ và SA vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là hình chiếu vuông góc của A trên SB và SC. Thế tích khối cầu ngoại tiếp hình chóp A.BCNM bằng
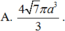
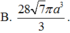
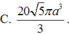
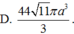
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C.
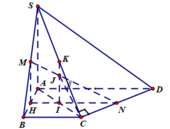

Ta dễ chứng minh được tam giácACD vuông tại C, từ đó chứng minh được CN vuông góc với mặt phẳng (SAC) hay C là hình chiếu vuông góc của N trên (SAC). Đường thẳng MN cắt mặt phẳng (SAC) tại J xác định như hình vẽ. Suy ra góc giữa MN và (SAC) là góc NJC .
IN là đương trung bình trong tam giác ACD suy ra IN=a, IH là đường trung bình trong tam giác ABC suy ra I H = 1 2 B C = a 2 . Dựa vào định lí Talet trong tam giác MHN ta được I J = 2 3 M H = 2 3 . 1 2 S A = 1 3 S A = a 3 . Dựa vào tam giác JIC vuông tại I tính được J C = 22 6 .
Ta dễ tính được C N = a 2 2 , J N = a 10 3 .
Tam giác NJC vuông tại C nên cos N J C ^ = J C J N = 55 10 .

Chọn B.
Dễ thấy AB ⊥ BC. Suy ra SB ⊥ BC, ∆ SMN đồng dạng với ∆ SCB, do đó
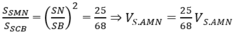

Chọn D.
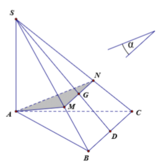
Do ( α ) đi qua G ∈ (SBC), song song với BC nên ( α ) cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
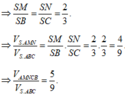
Do tam giác ABC vuông cân tại B, AC = a
2
nên ![]()
Do SA
⊥
(ABC) nên ![]()
![]()
Đáp án đúng : B