Cho số thực a ≢ 0 . Đặt b = ∫ - a a 1 2 a x e x d x . Tính I = ∫ 0...

PT

Pham Trong Bach

21 tháng 11 2018

Cho số thực a ≢ 0 . Đặt b = ∫ - a a 1 2 a + x e x d x . Tính I = ∫ 0 2 a e x 3 a - x theo a và b. A. I = b e a B. I = b e a C. I = b . e a D. I = a e b ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

21 tháng 11 2018

Đáp án C

Đúng(0)

PT

Pham Trong Bach

8 tháng 7 2018

Cho số thực a ≠ 0 . Đặt b = ∫ - a a 1 ( 2 a + x ) . e x d x . Tính I = ∫ 0 2 a e x 3 a - x d x theo a và b. ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

8 tháng 7 2018

Đáp án C.

Đúng(0)

TT

trần thị hoàng yến

20 tháng 10 2016 - olm

I) THỰC HIỆN PHÉP TÍNH a) 2x(x^2-4y) b)3x^2(x+3y) c) -1/2x^2(x-3) d) (x+6)(2x-7)+x e) (x-5)(2x+3)+x II phân tích đa thức thành nhân tử a) 6x^2+3xy b) 8x^2-10xy c) 3x(x-1)-y(1-x) d) x^2-2xy+y^2-64 e) 2x^2+3x-5 f) 16x-5x^2-3 g) x^2-5x-6 IIITÌM X BIẾT a)2x+1=0 b) -3x-5=0 c) -6x+7=0 d)(x+6)(2x+1)=0 e)2x^2+7x+3=0 f) (2x-3)(2x+1)=0 g) 2x(x-5)-x(3+2x)=26 h) 5x(x-1)=x-1 IV TÌM GTNN,GTLN. a) tìm giá trị nhỏ nhất x^2-6x+10 2x^2-6x b) tìm giá trị lớn nhất 4x-x^2-5...

Đọc tiếp

#Toán lớp 8

2

N

nguyenvankhoi196a

5 tháng 11 2017

Giải như sau.

(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y

⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !

Đúng(1)

DQ

Đường Quỳnh Giang

30 tháng 9 2018

$\left(x+6\right)\left(2x+1\right)=0$

<=> $\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}$

<=> $\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}$

Vậy....

hk tốt

^^

Đúng(1)

VT

vu tuan anh

4 tháng 3 2021 - olm

Câu hỏi 2 : Vì sao các số 1,2 ; -1,75 ; 0 ; 6 : là những số hữu tỉ ? Câu hỏi 3 : Số nguyên a có phải là số hữu tỉ không ? Vì sao ? Câu hỏi 4 : Trình bày cách biểu diễn một số hữu tỉ trên trục số . Câu hỏi 5 : Trình bày các bước thực hiện để so sánh hai số hữu tỉ x và y . Câu hỏi 6 : Trình bày các bước thực hiện để chỉ ra được dạng tổng quát của hữu tỉ X. Câu hỏi 7 : Nêu định...

Đọc tiếp

#Toán lớp 7

0

DH

diệp hoàng

18 tháng 4 2023

( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$

#Toán lớp 12

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 4 2023

Chọn C

Đúng(0)

DH

diệp hoàng

19 tháng 4 2023

em muốn hỏi cách làm ấy ạ? hướng giải là như nào ấy ạ

Đúng(0)

PT

Pham Trong Bach

30 tháng 7 2017

Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x

#Mẫu giáo

1

CM

Cao Minh Tâm

30 tháng 7 2017

Đáp án A

Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.

Cách giải : Đặt x = a – t => dx = –dt. Đổi cận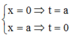

=>

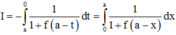
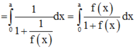
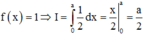
Đúng(0)

LN

lê nhật duẫn

26 tháng 3 2020

bài 7: chứng minh rằng

a. a^2(a+1)+2a(a+1) chia hết cho 6 với a là số nguyên

b. a(2a-3)-2a(a+1) chia hết cho 5 với a là số nguyên

c. x^2+2x+2>0 với mọi x

d. x^2-x+1>0 với mọi x

e. -x^2+4x-5<0 với mọi x

#Toán lớp 8

2

NM

Nguyễn Mạnh Nam

26 tháng 3 2020

Tớ làm cho bạn mà bạn toàn ko tick

Đúng(0)

NM

Nguyễn Mạnh Nam

26 tháng 3 2020

a)a²(a+1)+2a(a+1)=(a²+2a)(a+1)=a(a+2)(a+1)

Ta có Ta có a(a+1)(a+2) là 3 số tự nhiên liên tiếp =>a(a+1)(a+2)⋮3 (1)

Mà a(a+1)$⋮$2 (2)

Từ (1)(2) suy ra a(a+1)(a+2)⋮6

=>a²(a+1)+2a(a+1)⋮6

b)a(2a-3)-2a(a+1)=2a²-3a-2a²-2a=-5a

Vì -5 chia hết 5

=>-5a chia hết 5

c)x²+2x+2=x²+2x+1+1=(x+1)²+1

Vì (x+1)²≥0

<=>(x+1)²+1>0

d)x²-x+1=$x^2-\frac{2.1}{2}$+$\frac{1}{4}+\frac{3}{4}$=$\left(x-\frac{1}{2}\right)^2+\frac{3}{4}$

Vì $\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0$(đpcm)

e)-x²+4x-5=-(x²-4x+5)=-(x²-4x+4)-1=-(x-2)²-1

Vì -(x-2)²≤0=>-(x-2)²-1<0(đpcm)

rồi nhé

Đúng(0)

LN

lê nhật duẫn

26 tháng 3 2020

bài 7 : chứng minh rằng

a. a^2(a+1)+2a(a+1) chia hết cho 6 với a là số nguyên

b. a(2a-3)-2a(a+1) chia hết cho 5 với a là số nguyên

c. x^2+2x+2>0 với mọi x

d. x^2-x+1>0 với mọi x

e. -x^2+4x-5<0 với mọi x

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

26 tháng 3 2020

a) Ta có: $a^2\left(a+1\right)+2a\left(a+1\right)$

$=\left(a+1\right)\cdot\left(a^2+2a\right)$

$=a\cdot\left(a+1\right)\cdot\left(a+2\right)$

Vì a và a+1 là hai số nguyên liên tiếp nên $a\cdot\left(a+1\right)⋮2$(1)

Vì a; a+1 và a+2 là ba số nguyên liên tiếp nên $a\cdot\left(a+1\right)\cdot\left(a+2\right)⋮3$(2)

mà 2 và 3 là hai số nguyên tố cùng nhau(3)

nên từ (1); (2) và (3) suy ra $a\cdot\left(a+1\right)\cdot\left(a+2\right)⋮6\forall a\in Z$

hay $a^2\left(a+1\right)+2a\left(a+1\right)⋮6\forall a\in Z$(đpcm)

b) Ta có: $a\left(2a-3\right)-2a\left(a+1\right)$

$=2a^2-3a-2a^2-2a$

$=-5a⋮5\forall a\in Z$

hay $a\left(2a-3\right)-2a\left(a+1\right)⋮5\forall a\in Z$(đpcm)

c) Ta có: $x^2+2x+2$

$=x^2+2x+1+1$

$=\left(x+1\right)^2+1$

Ta có: $\left(x+1\right)^2\ge0\forall x\in Z$

$\Rightarrow\left(x+1\right)^2+1\ge1>0\forall x\in Z$

hay $x^2+2x+2>0\forall x\in Z$(đpcm)

d) Ta có: $x^2-x+1$

$=x^2-2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}$

$=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}$

Ta có: $\left(x-\frac{1}{2}\right)^2\ge0\forall x\in Z$

$\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\in Z$

hay $x^2-x+1>0\forall x\in Z$(đpcm)

e) Ta có: $-x^2+4x-5$

$=-\left(x^2-4x+5\right)$

$=-\left(x^2-4x+4+1\right)$

$=-\left(x-2\right)^2-1$

Ta có: $\left(x-2\right)^2\ge0\forall x\in Z$

$\Rightarrow-\left(x-2\right)^2\le0\forall x\in Z$

$\Rightarrow-\left(x-2\right)^2-1\le-1< 0\forall x\in Z$

hay $-x^2+4x-5< 0\forall x\in Z$

Đúng(0)

HV

Hoàng Văn Nam

13 tháng 1 2017 - olm

Bài 1 : Tính nhanh :

a) (-8).14.225

b) (-125).(-72).7

c) 47.69-31.(-47)

d) -4.2.6.25.(-7).5

e) -310.87+(-310).13

g) 42.48 -24.34

Bài 2 : Cho a.b=-60.Tính a.(-b);(-a).b;(-a).(-b)

Bài 3 Tìm x:

x(x-3)=0

Bài 4 : Tìm số nguyên x biết

a)x(x-30)<0

b)x(x-3)>0

c) (x+2)(x+5)<0

d) (x+2)(x+5)>0

#Toán lớp 6

3

SN

shi nit chi

13 tháng 1 2017

Bài 1 : Tính nhanh :

a) (-8).14.225

b) (-125).(-72).7

c) 47.69-31.(-47)

d) -4.2.6.25.(-7).5

e) -310.87+(-310).13

g) 42.48 -24.34

Bài 2 : Cho a.b=-60.Tính a.(-b);(-a).b;(-a).(-b)

Bài 3 Tìm x:

x(x-3)=0

Bài 4 : Tìm số nguyên x biết

a)x(x-30)<0

b)x(x-3)>0

c) (x+2)(x+5)<0

d) (x+2)(x+5)>0

bài này cũng dễ nhưng bn đăng nhiều quá nên mk ko làm hết đc

nên thui

chúc bn học gioi!#

Đúng(0)

S

Shizadon

13 tháng 1 2017

Rảnh quá nhỉ! không làm đi chúc bạn học giỏi

Đúng(0)

HY

Hoàng Yến

20 tháng 10 2016

I) THỰC HIỆN PHÉP TÍNHa) 2x(x^2-4y)b)3x^2(x+3y)c) -1/2x^2(x-3)d) (x+6)(2x-7)+xe) (x-5)(2x+3)+xII phân tích đa thức thành nhân tửa) 6x^2+3xyb) 8x^2-10xyc) 3x(x-1)-y(1-x)d) x^2-2xy+y^2-64e) 2x^2+3x-5f) 16x-5x^2-3g) x^2-5x-6IIITÌM X BIẾTa)2x+1=0b) -3x-5=0c) -6x+7=0d)(x+6)(2x+1)=0e)2x^2+7x+3=0f) (2x-3)(2x+1)=0g) 2x(x-5)-x(3+2x)=26h) 5x(x-1)=x-1IV TÌM GTNN,GTLN.a) tìm giá trị nhỏ nhất x^2-6x+10 2x^2-6xb) tìm giá trị lớn nhất 4x-x^2-5...

Đọc tiếp

#Toán lớp 8

2

NL

NHK Linh

23 tháng 10 2016

bn ko bik lm hay sao, hay là bn chỉ đăng đề lên thôi

Đúng(0)

NB

Nhók Bướq Bỉnh

2 tháng 11 2016

sao nhìu... z p , đăq từq câu 1 thôy nha p

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP