Cho hàm số y = x 3 + 2 m − 2 x 2 − 5 x + 1 . Tìm tất cả các giá trị thực của tham số m sao cho hàm số có hai điểm cực trị x 1 , x 2 ( x 1 < x 2 ) thỏa mãn x 1 − x 2 = − 2 .
A. 7 2
B. ‒1
C. 1 2
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
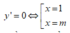
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
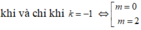

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
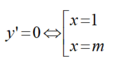
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 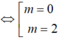
Chọn C.

Chọn C
Ta có: y ' = 2 x 2 - 2 m x - 2 ( 3 m 2 - 1 )
g ( x ) = x 2 - m x - 3 m 2 + 1 là tam thức bậc hai có ∆ = 13 m 2 - 4
Do đó hàm số có hai điểm cực trị khi và chỉ khi y ' có hai nghiệm phân biệt
⇔ g ( x ) có hai nghiệm phân biệt

x 1 ; x 2 là các nghiệm của g(x) nên theo định lý Vi-ét, ta có
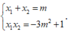

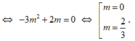
Đối chiếu với điều kiện (1), ta thấy chỉ m = 2 3 thỏa mãn yêu cầu bài toán
Đáp án C.
Ta có y ' = 3 x 2 + 4 m − 2 x − 5 ; y ' = 0 ⇔ 3 x 2 + 4 m − 2 x − 5 = 0 (*).
Phương trình (*) có a c < 0 nên luôn có hai nghiệm trái dấu .
Suy ra x 1 = − x 1 ; x 2 = x 2 .
Khi đó x 1 , x 2 là hai điểm cực trị của hàm số.
x 1 − x 2 = − 2 ⇔ − x 1 − x 2 = − 2 ⇔ x 1 + x 2 = 2 ⇔ − 4 m − 2 3 = 2 ⇔ m = 1 2