Giá trị nhỏ nhất của hàm số y = - x 2 + x - 6 x + 1 trên đoạn [0;3] bằng:
A. -6
B. -3
C. 3 - 4 2
D. 3 + 4 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 9 2018
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
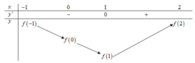
Nhận thấy
Để tìm 
ta so sánh f(-1) và f(2)
Theo giả thiết, 
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 
CM
16 tháng 3 2018
a) 
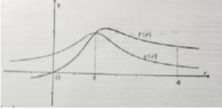
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
CM
28 tháng 7 2017
Chọn D
Ta có 3x.f(x) -
x
2
f
'
(
x
)
=
2
f
2
(
x
)
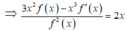
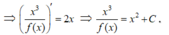
Thay x = 1 vào ta được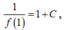 
vì f(1) =
1
3
nên suy ra C = 2
Nên 
Ta có: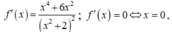 
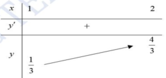
Khi đó, f(x) đồng biến trên [1;2]
Suy ra 
Suy ra 
CM
16 tháng 12 2018
Chọn C.
Nhận xét: Hàm số đã cho liên tục trên [0;3]
Ta có: 
nên hàm số đồng biến trên [0; 3].
.
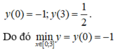
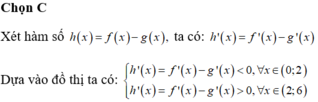
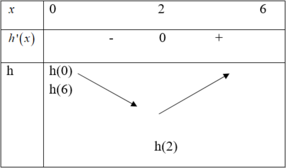
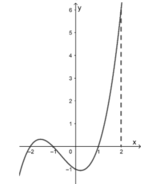
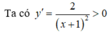
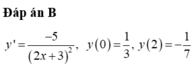
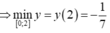
Chọn C
Lưu ý: Hàm số liên trục trên một Đoạn thì luôn có GTLN và GTNN trên đoạn đó Nên áp dụng bài toán tìm GTLN, GTNN của hàm số trên một đoạn, không lập BBT của hàm sô.
Hàm số y = - x 2 + x - 6 x + 1 liên tục trên đoạn [0;3]