Cho hình nón đỉnh (S) có đường sinh bằng 2 , đường cao bằng 1 . Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho:
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

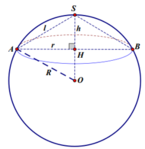
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1.
Suy ra r = l 2 - h 2 = 3
Góc ở đỉnh của hình nón là A S B = 2 A S H = 120 ° nên suy ra H ∈ S O (như hình vẽ).
Trong tam giác OAH vuông tại H ta có:
O A 2 = O H 2 + H A 2 ⇔ R 2 = R - h 2 + r 2 ⇔ R = h 2 + r 2 2 h = 2
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Chọn đáp án A.
Cách 2:
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1. (như hình vẽ)
Trong tam giác SAH vuông tại H ta có
cos A S H = S H S A = 1 2 ⇒ A S H = 60 °
Xét tam giác SOA có OS=OA=R và O S A = 60 °
Suy ra tam giác SOA đều.
Do đó R=OA=SA=2
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Chọn đáp án A.

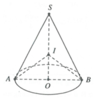
HD: Ta có tâm I của mặt cầu chính là tâm đường tròn ngoại tiếp tam giác SAB.


- Nếu H nằm ở nửa dưới đoạn SO thì \(R\ge\dfrac{SO}{2}=\dfrac{3}{2}\)
- Nếu H nằm ở nửa trên đoạn SO, thực hiện mặt cắt qua trục nón như hình vẽ
\(SO=OA=3\Rightarrow SOA\) vuông cân \(\Rightarrow SCH\) vuông cân
\(\Rightarrow CH=SH=3-OH=3-\left(R+IH\right)=3-R-\sqrt{R^2-CH^2}\)
\(\Rightarrow3-R=CH+\sqrt{R^2-CH^2}\le\sqrt{2\left(CH^2+R^2-CH^2\right)}=R\sqrt{2}\)
\(\Rightarrow R\left(\sqrt{2}+1\right)\ge3\Rightarrow R\ge\dfrac{3}{\sqrt{2}+1}=3\left(\sqrt{2}-1\right)\)
\(V_{min}=\dfrac{4}{3}\pi R_{min}^3=8,037\)
Đáp án đúng : A