Cho hàm số y = a x + b x + 1 có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
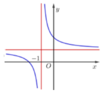
A. a < b < 0
B. b < 0 < a
C. 0 < b < a
D. 0 < a < b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Dựa vào hình vẽ, ta thấy rằng:
Đồ thị hàm số cắt trục Oy tại điểm có tung độ dương


Chọn C
Ta có: ![]()
Dựa vào đồ thị:
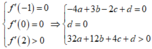

![]()
Dựa vào đồ thị, ta cũng có: ![]()
Từ (1),(2) suy ra a + c > 4a + c > 0.

Đáp án C
TCĐ: x = c < 0 , T C N : y = a > 0 . Đồ thị hàm số giao với trục oy tại điểm có tung độ − b c < 0 ⇒ b < 0
Đồ thị hàm số giao với trục ox tại điểm có hoành độ − b a > 0 ⇒ b < 0

Đáp án là D
Đồ thị f ' x có bảng biến thiên:
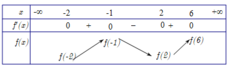
max [ − 2 ; 6 ] f ( x ) = max { f ( − 1 ) , f ( 6 ) } .

Đáp án D
Đồ thị hàm số có tiệm cận ngang y = a ⇒ a > 0 .
Ta có: c<0 do đồ thị hàm số có tiệp cận đứng x=c .
Đồ thị hàm số cắt trục tung tại điểm có tung độ − b c < 0 ⇒ b < 0 .

Đáp án B
Tiệm cân đứng x = − d c = − 1 ⇒ d = c .
Đồ thị hàm số đi qua điểm
0 ; − 1 d ⇒ − 1 d < 0 ⇒ d > 0.

Đáp án C
Phương pháp:
Đồ thị hàm số y = a x + b c x + d có hai đường tiệm cận: x = c và y = a, đồng thời cắt trục hoành tại điểm - b a ; 0
Cách giải:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng x = x0 < 0 ⇒ c < 0, đồ thị hàm số có tiệm cận ngang y = y_0 > 0 ⇒ a > 0
Đồ thị hàm số cắt trục hoành tại điểm
![]()
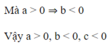
Đáp án D
Dựa vào hình vẽ, ta thấy rằng:
Đồ thị hàm số cắt trục O y tại điểm có tung độ dương ⇒ y 0 = b > 0
Đồ thị hàm số có TCN nằm phía trên trục O x ⇒ y = a > 0
Hàm số đã cho là hàm số nghịch biến ⇒ y ' = a − b x + 1 2 < 0 ⇔ a < b