Con lắc lò xo dao động điều hòa với phương trình: x = 5 cos ( 4 t ) cm. Vật nhỏ có khối lượng 20 g. Động năng cực đại của vật bằng
A. 1,6 mJ.
B. 0,8 mJ.
C. 0,2 mJ.
D. 0,4 mJ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Động năng cực đại của con lắc chính bằng cơ năng E = 0,5m ω 2 A 2 = 0,4 mJ

Một con lắc lò xo dao động theo phương trình x = 4cos10t
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}m.w^2.A^2=8.10^{-3}=8\left(mJ\right)\)
Vậy C đúng
Thế năng cực đại của con lắc lò xo:
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}.m.\omega^2.A^2=8.10^{-3}=8mJ\)
Chọn C

\(\Delta\varphi=\varphi_2-\varphi_1=\dfrac{\pi}{2}\)
\(A=\sqrt{A_1^2+A_2^2}=6\sqrt{2}\left(cm\right)\)
Phương trình dao động tổng hợp: \(x=6\sqrt{2}cos\left(5\pi t+\dfrac{\pi}{2}\right)cm\)
Cơ năng dao động của vật là:
\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}.0,2.\left(5\sqrt{10}\right)^2.\left(6\sqrt{2}.10^{-2}\right)^2=0,18\left(J\right)=180\left(mJ\right)\)
Chọn A.

+ Cơ năng của con lắc là: W = 1 2 k x 2 + 1 2 m v 2 = 1 2 k 0 , 045 − Δ l 2 + 1 2 m v 2
+ Mà Δ l = m g k
® 2 W = k 0 , 045 − m g k 2 + m .0 , 4 2 = 80.10 − 3
+ Giải phương trình trên ta được: m = 0 , 25 g m = 0 , 49 g ® chọn m = 0 , 25 g
+ T = 2 π m k = 2 π 0 , 25 100 = π 10 s
Đáp án B

ü Đáp án B
+ Cơ năng của con lắc là:
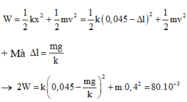
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → c h ọ n m = 0 , 25
T = 2 π m k = 2 π 0 . 25 100 = π 10 s
Động năng cực đại của con lắc chính bằng cơ năng
E = 0,5mω2A2 = 0,4 mJ.
Đáp án D