Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một con lắc lò xo dao động theo phương trình x = 4cos10t
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}m.w^2.A^2=8.10^{-3}=8\left(mJ\right)\)
Vậy C đúng
Thế năng cực đại của con lắc lò xo:
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}.m.\omega^2.A^2=8.10^{-3}=8mJ\)
Chọn C

\(\Delta\varphi=\varphi_2-\varphi_1=\dfrac{\pi}{2}\)
\(A=\sqrt{A_1^2+A_2^2}=6\sqrt{2}\left(cm\right)\)
Phương trình dao động tổng hợp: \(x=6\sqrt{2}cos\left(5\pi t+\dfrac{\pi}{2}\right)cm\)
Cơ năng dao động của vật là:
\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}.0,2.\left(5\sqrt{10}\right)^2.\left(6\sqrt{2}.10^{-2}\right)^2=0,18\left(J\right)=180\left(mJ\right)\)
Chọn A.

+ Cơ năng của con lắc là: W = 1 2 k x 2 + 1 2 m v 2 = 1 2 k 0 , 045 − Δ l 2 + 1 2 m v 2
+ Mà Δ l = m g k
® 2 W = k 0 , 045 − m g k 2 + m .0 , 4 2 = 80.10 − 3
+ Giải phương trình trên ta được: m = 0 , 25 g m = 0 , 49 g ® chọn m = 0 , 25 g
+ T = 2 π m k = 2 π 0 , 25 100 = π 10 s
Đáp án B

ü Đáp án B
+ Cơ năng của con lắc là:
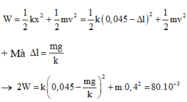
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → c h ọ n m = 0 , 25
T = 2 π m k = 2 π 0 . 25 100 = π 10 s

+ Cơ năng của con lắc là:

+ Mà ∆ l = m g k
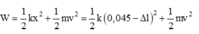
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → chọn m = 0,25 g
T = 2 π m k = 2 π 0 . 25 100 = π 10 s
ü Đáp án B

Đáp án C
Phương pháp: Sử dụng lí thuyết về dao động điều hòa của con lắc lò xo
Cách giải:
+ Cơ năng dao động của con lắc lò xo:

+ Ta có công thức độc lập với thời gian giữa gia tốc và vận tốc:
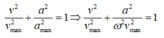
Do đó ta tính được tần số góc theo công thức sau:
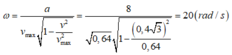
=> Biên độ dao động A = vmax/ω = 80/20 = 4 cm; li độ tại thời điểm ban đầu của vật là x = -a/ω2 = - 2 cm => Pha ban đầu của vật là φ = -2π/3 => Chọn C
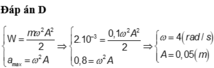
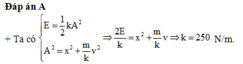
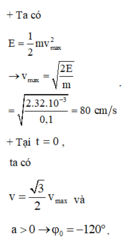
Động năng cực đại của con lắc chính bằng cơ năng
E = 0,5mω2A2 = 0,4 mJ.
Đáp án D