Tìm số nguyên dương n, biết: 3.27 > 3n ≥ 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
tìm số nguyên dương n, biết:
a) 25<5n<625
b)3.27>3nlớn hơn, bằng 9
c)16 bé hơn, bằng 8n bé hơn, bằng 64
1
21 tháng 2 2020
a) \(25< 5^n< 625\)
\(25=5^2;625=5^4\)
=> \(5^2< 5^n< 5^4\)
=> 2 < n < 4
=> n = 3
b) \(9\le3^n< 3.27\)
\(9=3^2;3.27=3.3^3=3^4\)
=> \(3^2\le3^n< 3^4\)
=> n = 2; hoặc n = 3
c) \(16\le8^n\le64\)
\(16=8.2;64=8^2\)
=> \(8.2\le8^n\le8^2\)
=> n = 2
NT
1
AH
Akai Haruma
Giáo viên
26 tháng 7 2021
Lời giải:
Để $\frac{3n+9}{n-4}$ là số hữu tỉ dương thì có 2 TH xảy ra:
TH1:
\(\left\{\begin{matrix} 3n+9>0\\ n-4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} n>-3\\ n>4\end{matrix}\right.\Leftrightarrow n>4\)
TH2:
\(\left\{\begin{matrix} 3n+9< 0\\ n-4< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} n< -3\\ n< 4\end{matrix}\right.\Leftrightarrow n< -3\)
PT
1
NA
1
HP
22 tháng 11 2015
3n+14 chia hết chi n+1
=>3(n+1)+11 chia hết cho n+1
=>11 chia hết cho n+1
=>n+1 thuộc Ư(11)={1;11}
+)n+1=1=>n=0
+)n+1=11=>n=10
vậy....
NQ
0
9 tháng 8 2019
a) Ta có: A = \(\frac{n+9}{n-4}=\frac{\left(n-4\right)+13}{n-4}=1+\frac{13}{n-4}\)
Để A \(\in\)Z <=> 13 \(\in\)n - 4 <=> n - 4 \(\in\)Ư(13) = {1; -1; 13; -13}
Với : +) n - 4 = 1 => n = 1 + 4 = 5
+) n - 4 = -1 => n = -1 + 4 = 3
+) n - 4 = 13 => n = 13 + 4 = 17
+) n - 4 = -13 => n= -13 + 4 = -9
Vậy ...
b) Ta có: B = \(\frac{3n+5}{n-1}=\frac{3\left(n-1\right)+8}{n-1}=3+\frac{8}{n-1}\)
Để B \(\in\)Z <=> 8 \(⋮\)n - 1 <=> n - 1 \(\in\)Ư(8) = {1; -1; 2; -2; 4; -4; 8; -8}
Lập bảng :
| n - 1 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| n | 2 | 0 | 3 | -1 | 5 | -3 | 9 | -7 |
Vậy ...
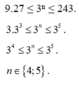
Từ đề bài suy ra 34 > 3n ≥ 32, tìm được n ∈ {2; 3}