Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B. Biết AB=BC=
a
3
,
![]() và khoảng cách từ A đến mặt phẳng (SBC) bằng
a
2
.Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng
và khoảng cách từ A đến mặt phẳng (SBC) bằng
a
2
.Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng
![]()
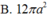
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

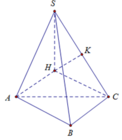
Đáp án B
Dựng hình vuông ABCH
Ta có: A B ⊥ A H A B ⊥ S A ⇒ A B ⊥ S H , tương tự B C ⊥ S H
Do đó S H ⊥ A B C
Lại có A H / / B C ⇒ d A ; S B C = d H ; S B C
Dựng H K ⊥ S C ⇒ d H ; S B C − H K = a 2
Do đó 1 S H 2 = 1 H K 2 − 1 H C 2 ⇒ S H = a 6 .
Tứ giác ABCH nội tiếp nên R S . A B C = R S . A B C H = S H 2 4 + r 2 d
= S H 2 4 + A C 2 2 = a 3 ⇒ S = 4 π R 2 = 12 π a 2 .

Đáp án C
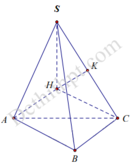
Dựng hình vuông ABCH
Ta có A B ⊥ A H A B ⊥ S A ⇒ A B ⊥ S H , tương tự B C ⊥ S H
Do đó S H ⊥ A B C
Lại có A H / / B C ⇒ d A ; S B C = d H ; S B C
Dựng H K ⊥ S C ⇒ d H ; S B C = H K = a 2
Do đó 1 S H 2 = 1 H K 2 − 1 H C 2 ⇒ S H = a 30 5
Tứ giác ABCH nội tiếp nên R S . A B C = R S . A B C H = S H 2 4 + r d 2
= S H 2 4 + A C 2 2 = a 2 ⇒ S = 4 π R 2 = 8 π a 2

Chọn đáp án D
+ Gọi H là trung điểm SB. Do tam giác SAB vuông tại A, SBC vuông tại C suy ta HA = HB = HS = HC
Suy ra H là tâm mặt cầu.
+ Gọi I là hình chiếu của H lên (ABC). Do HA = HB = HC , suy ra IA = IB = IC
Suy ra I là trung điểm AC. Gọi P là trung điểm BC, do tam giác ABC vuông cân, suy ra
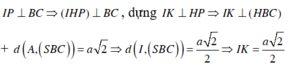
Áp dụng hệ thức
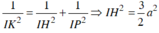
\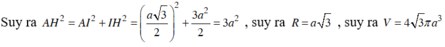

Đáp án B
HDG:
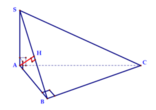
![]()
Dễ dàng chứng minh ∆ S B C vuông tại B
![]()
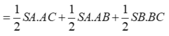
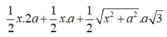
![]()
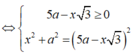
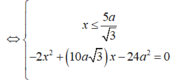
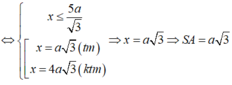
Ta có (SAB) ⊥ (SBC) theo giao tuyến SB. Kẻ
![]()
![]()
Đáp án đúng : B