Question

[Pham Trong Bach]

Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng ${\Delta }_1:\left\{\begin{array}{l}x=-3+2t\\ y=1-t\\ z=-1+4t\end{array}\right.$ và ${\Delta }_2:\frac{x+4}{3}=\frac{y+2}{2}=\frac{z-4}{-1}$. Khẳng định nào sau đây đúng?

A. ${\Delta }_1,{\Delta }_2$ chéo nhau và vuông góc nhau

B. ${\Delta }_1$ cắt và không vuông góc với  ${\Delta }_2$

C. ${\Delta }_1$ cắt và vuông góc với  ${\Delta }_2$

D. ${\Delta }_1$ và ${\Delta }_2$ song song với nhau

Answer 1

[Cao Minh Tâm]

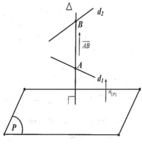
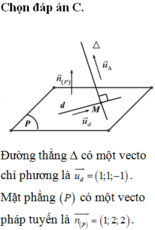
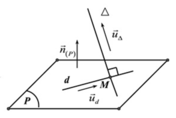
Đáp án C.

Phương trình tham số của đường thẳng  Δ 2 : x = − 4 + 3 t ' y = − 2 + 2 t ' z = 4 − t ' , t ' ∈ ℝ

Đường thẳng  lần lượt có vecto chỉ phương (VTCP) là u 1 → = 2 ; − 1 ; 4  và  u 2 → = 3 ; 2 ; − 1   . Suy ra u 1 → . u 2 → = 2.3 + − 1 .2 + 4. − 1 = 0  và  Δ 1 ⊥ Δ 2   . Loại B, D.

Xét hệ phương trình

− 3 + 2 t = − 4 + 3 t ' 1 − t = − 2 + 2 t ' − 1 + 4 t = 4 − t ' ⇔ 2 t − 3 t ' = − 1 t + 2 t ' = 3 4 t + t ' = 5 ⇔ t = 1 t ' = 1 ⇒ Δ 1 , Δ 2

 cắt nhau

Vậy Δ 1  cắt và vuông góc với Δ 2 .