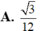
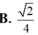
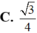
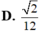
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
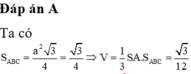
Đáp án A
Ta có S A B C = a 2 3 4 = 3 4 ⇒ V = 1 3 S A . S A B C = 3 12
Đáp án D
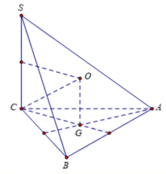
Ta có C G = 2 3 3 a 2 − 3 a 2 2 = a 3
Bán kính khối cầu R = C O = S C 2 2 + C G 2 = a 2 + a 3 2 = 2 a
Thể tích khối cầu V = 4 3 π R 3 = 4 3 π 2 a 3 = 32 π a 3 3
Gọi M là trung điểm SA và O là tâm đáy \(\Rightarrow AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AM=\dfrac{a}{2}\)
Qua O kẻ đường thẳng d song song SA, trong mặt phẳng (SAO) qua M kẻ đường thẳng song song AO cắt d tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(R=IA=\sqrt{IM^2+AM^2}=\sqrt{AO^2+AM^2}=\dfrac{a\sqrt{21}}{6}\)
Đáp án C
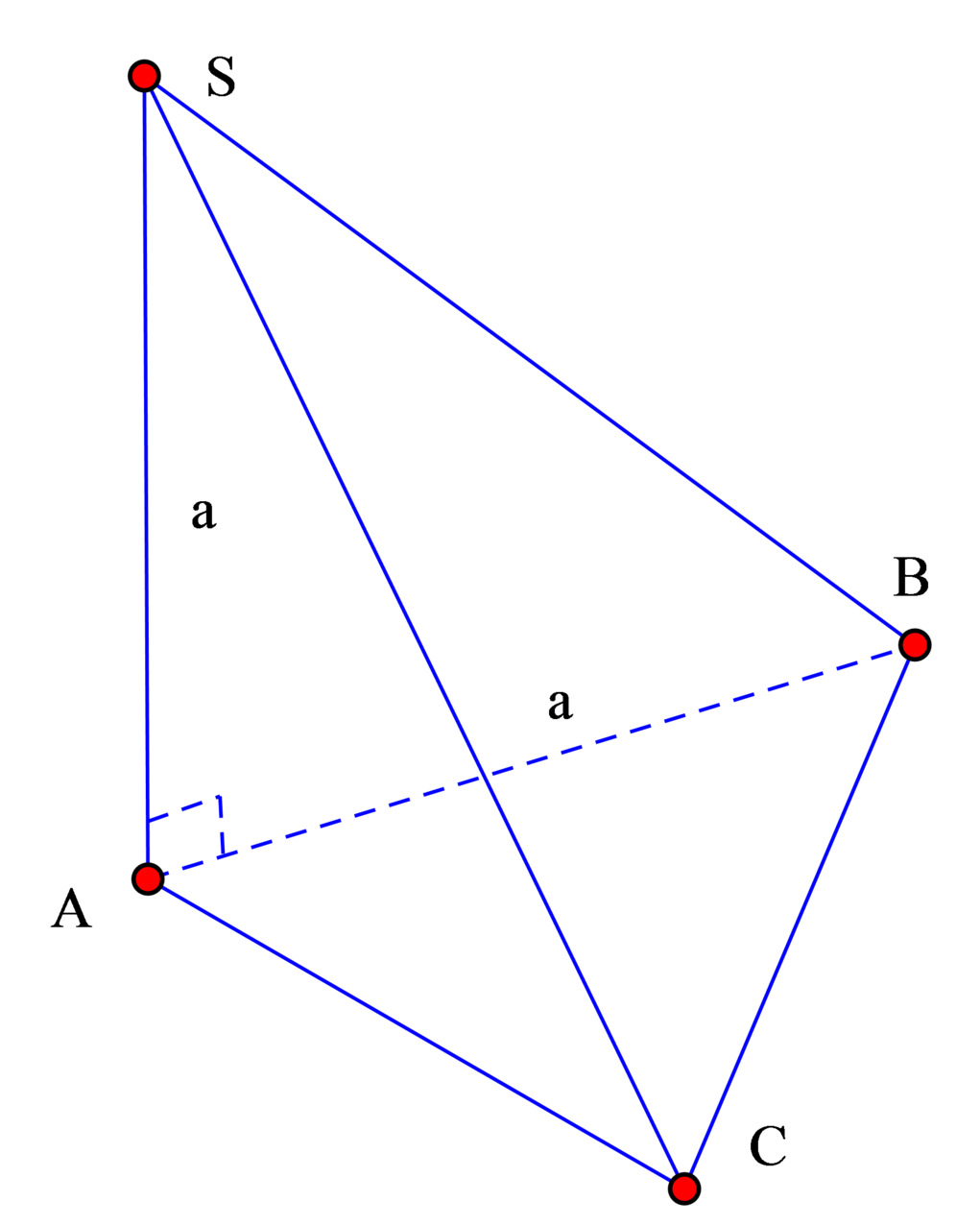
Ta có diện tích tam giác đều cạnh a là S = a 2 3 4
⇒ V S . A B C = 1 3 S A . d t A B C = 1 3 a . a 2 3 4 = a 3 3 12
