Cho hình vuông ABCD có diện tích bằng 36, A B → là một vectơ chỉ phương của đường thẳng y=0, các điểm A, B, C lần lượt nằm trên đồ thị hàm số y = log a x , y = 2 log a x , y = 3 log a x . Tìm a.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

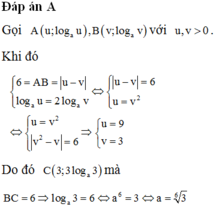

Đáp án A
Gọi A ( u ; log a ; u ) , B ( v ; log a ; v ) với u,v>0
Khi đó 
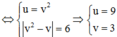
Do đó
C
(
3
;
3
log
a
;
3
)
mà BC = 6 => ![]()

Các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x y = log a 3 x với (x>0;a>1)
⇒ Giả sử A ( x 1 ; log a x 1 ) ; B ( x 2 ; 2 log a x 2 ) ; C ( x 3 ; 3 log a x 3 )
Do AB//Ox nên log a x 1 = log a x 2 ⇔ x 1 = x 2 2
Khi đó:
A ( x 2 2 ; log a x 2 ) ; B ( x 2 ; 2 log a x 2 ) ; ⇒ A B = x 2 2 - x 2
Hình vuông ABCD có diện tích bằng 36
![]()


⇔ x 2 = 3 ⇒ x 1 = 9
![]()
![]()
Mặt khác, do AB // Ox nên BC // Oy ⇒ x 3 = 3
![]()
C ( 3 ; log a x 3 )
![]()
![]()
![]()
Chọn đáp án D.

Đáp án D.
Do AB//Ox => A, B nằm trên đường thẳng y = m ( m ≠ 0 )
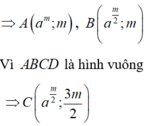
Do SABCD = 36
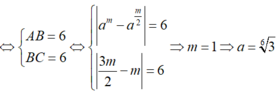 .
.