Từ các chữ số thuộc tập hợp S = {1;2;3;4;5;6;7;8;9} có bao nhiêu số có 9 chữ số khác nhau sao cho chữ số 1 đứng trước chữ số 2, chữ số 3 đứng trước chữ số 4, chữ số 5 đứng trước chữ số 6 ?
A. 7560.
B. 272160.
C. 45360.
D. 362880.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2017
Tập S có 9 4 phần tử. Ta có
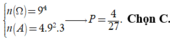
Thật vậy: Gọi số thỏa mãn biến cố là 
CM
27 tháng 1 2018
Đáp án C
Số các số gồm 5 chữ số đôi 1 khác nhau là: 5! = 120 số
Trong mỗi hàng do các số có khả năng xuất hiện như nhau nên mỗi số xuất hiện 120 : 5 = 24 lần
S = (5 + 6 + 7 + 8 + 9).24.11111 = 9333240
CM
7 tháng 3 2019
Đáp án C
Số các số gồm 5 chữ số đôi 1 khác nhau là: 5! = 120 số
Trong mỗi hàng do các số có khả năng xuất hiện như nhau nên mỗi số xuất hiện 120:5=24 lần
S = ( 5 + 6 + 7 + 8 + 9 ) .24.11111 = 9333240
CM
2 tháng 6 2018
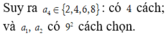
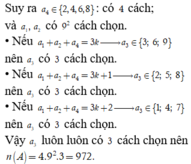
Đáp án C
Số các số gồm 5 chữ số đôi 1 khác nhau là: 5! = 120 số
Trong mỗi hàng do các số có khả năng xuất hiện như nhau nên mỗi số xuất hiện 120:5=24 lần
⇒ S= 9333240
CM
21 tháng 8 2018
Đáp án C
Số phần tử của tập S là 5! = 120 số.
Mỗi số 5, 6, 7, 8, 9 có vai trò như nhau và xuất hiện ở hàng đơn vị 4! = 24 lần
Tổng các chữ số xuất hiện ở hàng đơn vị là 4!.(5 + 6 + 7 + 8 + 9) = 840
Tương tự với các chữ số hàng chục, hàng tram, hàng nghìn và hàng chục nghìn.
Vậy tổng tất cả các số thuộc tập S là 840.(104+103+102+10+1) = 9333240
24 tháng 3 2023
Tổng tập hợp \(S\) là:
\(S=\left\{5+6+7+8+9\right\}\\ S=35\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
Có \(A_8^5=6720\) số bất kì (kể cả bắt đầu bằng 0)
Do vai trò của các chữ số là như nhau, nên ở mỗi vị trí, mỗi chữ số xuất hiện: \(67220:5=1344\) lần
Ta chọn 1 số làm đại diện tính toán, ví dụ số 3, do số 3 xuất hiện ở các hàng chục ngàn, ngàn, trăm, chục, đơn vị mỗi hàng đều 1344 lần nên tổng giá trị của số 3 là:
\(1344.\left(3.10000+3.1000+3.100+3.10+3.1\right)=1344.11111.3\)
Do vai trò các chữ số là giống nhau nên tổng các chữ số là:
\(S_1=1344.11111.\left(0+3+4+5+6+7+8+9\right)\)
Bây giờ ta lập các số có số 0 đứng đầu, nó đồng nghĩa với việc lập số có 4 chữ số từ các chữ số 3,4,5,6,7,8
Số số lập được là: \(A_7^4=840\) số
Do vai trò các chữ số như nhau nên mỗi vị trí mỗi chữ số xuất hiện \(840:4=210\) lần
Tương tự như trên, ta có tổng trong trường hợp này là:
\(S_2=210.1111.\left(3+4+5+6+7+8+9\right)\)
Giờ lấy \(S_1-S_2\) là được
Chọn C
Xếp chữ số 1 và 2 vào hai vị trí, do không giao hoán nên có: C 9 2 (cách).
Tương tự xếp chữ số 3 và 4 có C 7 2 (cách), xếp chữ số 5 và 6 có C 5 2 (cách).
Ba chữ số 7,8,9 hoán vị vào ba vị trí còn lại, có số cách xếp là 3! (cách).
Vậy số các chữ số thỏa mãn bài toán là: C 9 2 C 7 2 C 5 2 .3! = 45360(số).