Trong không gian Oxyz cho ba điểm , và . Tìm tọa độ điểm I trên mặt phẳng (Oxy) sao cho biểu thức đạt giá trị nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
18 tháng 9 2019
Gọi I(a,b,c) là tâm mặt cầu ta có
![]()
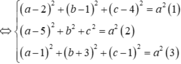
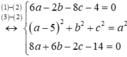
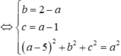
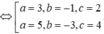
Vậy có tất cả 2 mặt cầu thoả mãn.
Chọn đáp án C.

MH
2 tháng 2 2021
Ta có: \(\overrightarrow{BC}=\left(-1;-6;3\right)\)
Đường thẳng song song với \(BC\) nên nó nhận \(\overrightarrow{BC}\) làm VTCP
\(\Rightarrow\) Phương trình tham số của đường thẳng đi qua \(A\) và song song với \(BC\) là: \(\left\{{}\begin{matrix}x=1-t\\y=-1-6t\\z=3+3t\end{matrix}\right.\quad\left(t\in R\right)\).
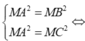
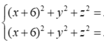
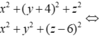
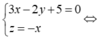
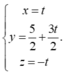
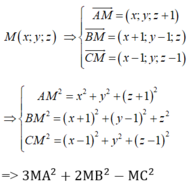
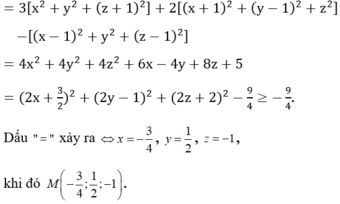






Đáp án B.
Gọi M là điểm thỏa mãn
M A → − 2 M B → + 5 M C → = 0 ⇔ M − 27 4 ; 1 ; 21 4
Khi đó
I A → − 2 I B → + 5 I C → = I M → + M A → − 2 I M → + 5 I M → + 5 M C → = 4 I M → + 0 → = 4 I M →
Biểu thức I A → − 2 I B → + 5 I C → đạt giá trị nhỏ nhất ⇔ I M → nhỏ nhất => I là hình chiếu của M trên mặt phẳng O x z ⇔ I − 27 4 ; 0 ; 21 4 .
Bài toán tổng quát: Trong không gian cho các điểm A 1 , A 2 ,..., A n và mặt phẳng P . Tìm điểm I trên mặt phẳng P sao cho biểu thức k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → đạt giá trị nhỏ nhất, trong đó k 1 , k 2 ,..., k n là những số thực và ∑ i = 0 n k i ≠ 0 .
Cách giải:
- Tìm điểm M thỏa mãn k 1 M A 1 → + k 2 M A 2 → + ... + k n M A n → = 0 .
- Khi đó k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → = ∑ i = 1 n k i I M → .
- Do đó k 1 I A 1 → + k 2 I A 2 → + ... + k n I A n → đạt giá trị nhỏ nhất ⇔ I M → nhỏ nhất => I là hình chiếu vuông góc của M trên P .