Cho n là số nguyên dương và a > 0 , a ≠ 1.
Tìm n sao cho: log a 2019 + log a 2019 + ... + log a n 2019 = 2033136 log a 2019.
A. n = 2017
B. n = 2016
C. n = 2018
D. n = 2019
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
a) Ta có: \(M = {a^{{{\log }_a}M}},N = {a^{{{\log }_a}N}} \Rightarrow MN = {a^{{{\log }_a}M}}.{a^{{{\log }_a}N}} = {a^{{{\log }_a}M + {{\log }_a}N}}\)
Mặt khác: \(MN = {a^{{{\log }_a}\left( {MN} \right)}}\)
Vậy \({a^{{{\log }_a}M + {{\log }_a}N}} = {a^{{{\log }_a}\left( {MN} \right)}} \Leftrightarrow {\log _a}M + {\log _a}N = {\log _a}\left( {MN} \right)\)
b)
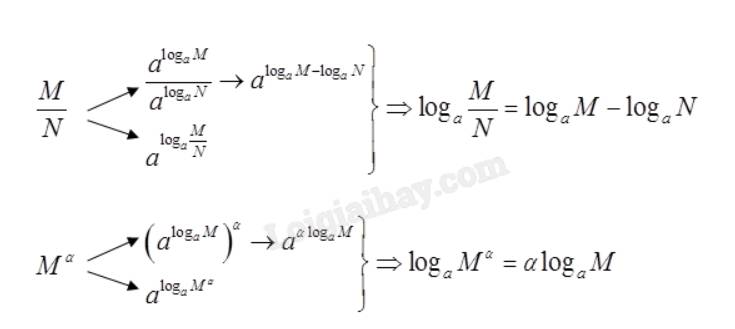

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)

\(a,a^{log_ab^{\alpha}}=c\Leftrightarrow log_ac=log_ab^{\alpha}\Leftrightarrow c=b^{\alpha}\Rightarrow a^{log_ab^{\alpha}}=b^{\alpha}\\ a^{\alpha log_ab}=c\Leftrightarrow\alpha log_ab=log_ac\Leftrightarrow log_ab^{\alpha}=log_ac\Leftrightarrow b^{\alpha}=c\Rightarrow a^{\alpha log_ab}=b^{\alpha}\\ \Rightarrow a^{log_ab^{\alpha}}=a^{\alpha log_ab}\)
\(b,a^{log_ab^{\alpha}}=a^{\alpha log_ab}\\ \Rightarrow log_ab^{\alpha}=\alpha log_ab\)
Đáp án B
Ta có: log a 2019 + log a 2019 + ... + log a n 2019
= log a 2019 + 2 log 2019 + ... + n log a 2019
= log a 2019 1 + 2 + ... + n = n 2 n + 1 log a 2019
= 2033136 log a 2019 ⇒ n 2 n + 1 = 2033136
⇔ n 2 + n − 4066272 = 0 ⇔ n = 2016 n = − 2017 ⇒ n = 2016.