Tìm hệ số của x 97 trong khai triển đa thức x - 2 100
A. 1293600
B. -1293600
C. ( - 2 ) 97 C 100 97
D. 2 97 C 100 97
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

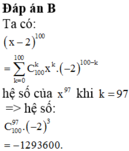

\(\left(1+x\right)^n=\sum\limits^n_{k=0}C_n^kx^k\)
Hệ số của 2 số hạng liên tiếp là \(C_n^k\) và \(C_n^{k+1}\)
\(\Rightarrow7C_n^k=5C_n^{k+1}\Leftrightarrow\frac{7n!}{k!.\left(n-k\right)!}=\frac{5n!}{\left(k+1\right)!\left(n-k-1\right)!}\)
\(\Leftrightarrow\frac{7}{n-k}=\frac{5}{k+1}\Leftrightarrow7k+7=5n-5k\)
\(\Leftrightarrow5n=12k+7\Rightarrow n=\frac{12k+7}{5}\)
\(\Rightarrow n_{min}=11\) khi \(k=4\)
2/ \(\left(x-2\right)^{100}=\sum\limits^{100}_{k=0}C_{100}^kx^k.\left(-2\right)^{100-k}\)
\(a_{97}\) là hệ số của \(x^{97}\Rightarrow k=97\)
Hệ số là \(C_{100}^{97}.\left(-2\right)^3\)

Tổng các hệ số của các hạng tử của đa thức P(x) bằng giá trị của P(x) tại x = 1
=> Tổng các hệ số của các hạng tử của đa thức P(x) là:
(10. 12 - 10. 1)100 = 0100 = 0

Tổng các hệ số của các hạng tử cửa đa thức = giá trị của đa thức khi x=1.
Vậy, tổng các hệ số của các hạng tử cửa đa thức = P(1)
=(10.12-10.1)100=0100=0
Vậy, tổng các hệ số của các hạng tử cửa đa thức là 0.

Đáp án C
Ta có: C n k = C n n − k nên đẳng thức:
C n 2 C n n- 2 + 2 C n 2 C n 3 + C n 3 C n n − 3 = 100 ⇔ C n 2 2 + 2 C n 2 C + C n 3 2 = 100
⇔ C n 2 + C n 3 2 = 100 ⇔ C n + 1 3 2 = 100 ⇔ C n + 1 3 = 10 ⇒ n = 4
Số hạng tổng quát trong khai triển: x − 1 x 4 = x + − 1 x 4 là:
T k + 1 = C 4 k x 4 − k − 1 x k = − 1 k C 4 k x 4 − k . x − k = − 1 k C 4 k x 4 − 2 k
Số hạng không chứa x ứng với k thỏa mãn:
4 − 2 k = 0 ⇔ k = 2 và có giá trị là: − 1 2 . C 4 2 = 6

Giả thiết tương đương:
\(C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n}+C_{2n+1}^{2n+1}=2^{100}\) (thay \(1=C_{2n+1}^{2n+1}\))
Mặt khác:
\(C_{2n+1}^{2n+1}=C_{2n+1}^0\)
\(C_{2n+1}^{2n}=C_{2n+1}^1\)
....
\(C_{2n+1}^{n+1}=C_{2n+1}^n\)
Cộng vế:
\(\Rightarrow C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n+1}=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n\)
\(\Rightarrow2\left(C_{2n+1}^{n+1}+...+C_{2n+1}^{2n+1}\right)=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^{2n+1}\)
\(\Rightarrow2.2^{100}=2^{2n+1}\) (đẳng thức cơ bản: \(\sum\limits^n_{k=0}C_n^k=2^n\))
\(\Leftrightarrow2^{101}=2^{2n+1}\)
\(\Rightarrow2n+1=101\)
\(\Rightarrow n=50\)
SHTQ trong khai triển: \(C_{50}^k.\left(x^{-3}\right)^k.\left(x^2\right)^{50-k}=C_{50}^kx^{100-5k}\)
\(100-5k=20\Rightarrow k=16\)
Hệ số: \(C_{50}^{16}\)

Số hạng tổng quát của khai triển: \(C_7^k.x^k.2^{7-k}\)
Số hạng chứa \(x^5\Leftrightarrow k=5\)
Hệ số của số hạng đó là: \(C_7^5.2^2=...\)