Cho hai parabol P 1 : y = x 2 3 x - 2 và P 2 : y = x 2 5 x 4 . Phép...

PT

Pham Trong Bach

4 tháng 3 2018

Cho hai parabol P 1 : y = x 2 + 3 x - 2 và P 2 : y = x 2 + 5 x + 4 . Phép tịnh tiến theo v → = a ; b biến ( P 1 ) thành ( P 2 ) thì a+b bằng: A. 3 B. -3 C. -1 D....

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

4 tháng 3 2018

Đúng(0)

KK

Kim Khánh Linh

16 tháng 5 2021 - olm

1) Giải hệ phương trình sau: $\left\{\begin{array}{l}\dfrac{2}{x-y}+\sqrt{y+1}=4 \\ \dfrac{1}{x-y}-3 \sqrt{y+1}=-5\end{array}\right.$. 2) Cho Parabol $(P): y=x^{2}$ và đường thẳng $(d): y=2(m-1) x-m^{2}+2 m$ ($m$ là tham số) a) Tìm tọa độ giao điểm của Parabol $(P)$ và đường thẳng $(d)$ khi $m=2$. b) Tìm $m$ để đường thẳng $(d)$ và Parabol $(P)$ cắt nhau tại hai điểm phân biệt có hoành độ $x_{1} , x_{2}$ đối...

Đọc tiếp

#Toán lớp 9

4

LD

l҉o҉n҉g҉ d҉z҉

16 tháng 5 2021

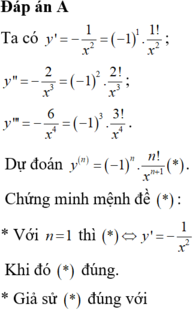
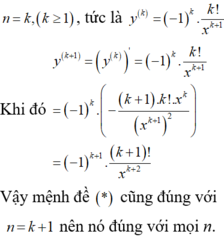
1) ĐK $\hept{\begin{cases}x\ne y\\y\ge-1\end{cases}}$

Đặt $\hept{\begin{cases}\frac{1}{x-y}=a\left(a\ne0\right)\\\sqrt{y+1}=b\left(b\ge0\right)\end{cases}}$hệ phương trình đã cho trở thành

$\hept{\begin{cases}2a+b=4\\a-3b=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+b=4\\2a-6b=-10\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=14\\2a+b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=2\end{cases}\left(tm\right)}$

$\Rightarrow\hept{\begin{cases}\frac{1}{x-y}=1\\\sqrt{y+1}=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=1\\y+1=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\y=3\end{cases}}\left(tm\right)$

Vậy ...

Đúng(0)

NA

Nguyễn Anh Tuấn

16 tháng 5 2021

ĐKXĐ: x ≠ y ; y ≥ − 1 Đặt 1 x − y = a ; √ y + 1 = b (ĐK: a ≠ 0 ; b ≥ 0 ) Khi đó hệ phương trình trở thành { 2 a + b = 4 a − 3 b = − 5 ⇔ { 6 a + 3 b = 12 a − 3 b = − 5 ⇔ { 7 a = 7 b = 4 − 2 a ⇔ { a = 1 ( tm ) b = 2 ( tm ) Với ⎧ ⎪ ⎨ ⎪ ⎩ a = 1 b = 2 ⇒ ⎧ ⎪ ⎨ ⎪ ⎩ 1 x − y = 1 √ y + 1 = 2 ⇒ { x − y = 1 y + 1 = 4 ⇔ { x − 3 = 1 y = 3 ⇔ { x = 4 ( tm ) y = 3 ( tm ) Vậy hệ phương trình đã cho có nghiệm { x = 4 y = 3 . 2) Xét phương trình hoành độ giao điểm giữa đường thẳng ( d ) và Parabol ( P ) là: x 2 = 2 ( m − 1 ) x − m 2 + 2 m ⇔ x 2 − 2 ( m − 1 ) x + m 2 − 2 m = 0 (1) a) Với m = 2 phương trình (1) trở thành: x 2 − 2 ( 2 − 1 ) x + 2 2 − 2.2 = 0 ⇔ x 2 − 2 x = 0 ⇔ x ( x − 2 ) = 0 ⇔ [ x = 0 x = 2 - Với x = 0 ⇒ y = 0 2 = 0 ⇒ A ( 0 ; 0 ) - Với x = 2 ⇒ y = 2 2 = 4 ⇒ B ( 2 ; 4 ) Vậy khi m = 2 thì ( P ) cắt ( d ) tại hai điểm phân biệt A ( 0 ; 0 ) ; B ( 2 ; 4 ) . b) Ta có: Δ ′ = b ′ 2 − a c = [ − ( m − 1 ) ] 2 − ( m 2 − 2 m ) = m 2 − 2 m + 1 − m 2 + 2 m = 1 > 0 Do Δ ′ > 0 nên phương trình (1) luôn có hai nghiệm phân biệt x 1 ; x 2 với mọi m . ⇒ Đường thẳng ( d ) luôn cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ x 1 ; x 2 với mọi m . Khi đó theo hệ thức Viet, ta có: { x 1 + x 2 = 2 m − 2 x 1 x 2 = m 2 − 2 m Để đường thẳng ( d ) cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ đối nhau ⇔ x 1 + x 2 = 0 ⇔ 2 m − 2 = 0 ⇔ m = 1 ( tm ) Vậy m = 1 thì đường thẳng ( d ) luôn cắt Parabol ( P ) tại hai điểm phân biệt có hoành độ đối nhau.

Đúng(0)

KK

Kim Khánh Linh

15 tháng 5 2021 - olm

1) Giải hệ phương trình $\left\{\begin{array}{l}2 \sqrt{x}+\dfrac{3}{y-1}=5 \\ 4 \sqrt{x}-\dfrac{1}{y-1}=3\end{array}\right.$ 2) Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): y=x^{2}$ và đường thẳng $(d): y=m x-1$, với $m$ là tham số ($m \neq 0$) a) Khi $m=3$, tìm tọa độ giao điểm của đường thẳng $(d)$ và parabol $(P)$. b) Tìm tất cả các giá trị khác 0 của tham số $m$ để đường thẳng $(d)$ cắt parabol $(P)$ tại hai...

Đọc tiếp

#Toán lớp 9

2

LD

l҉o҉n҉g҉ d҉z҉

16 tháng 5 2021

1) ĐK $\hept{\begin{cases}x\ge0\\y\ne1\end{cases}}$

Đặt $\hept{\begin{cases}2\sqrt{x}=a\left(a\ge0\right)\\\frac{1}{y-1}=b\left(b\ne0\right)\end{cases}}$hệ phương trình đã cho trở thành

$\hept{\begin{cases}a+3b=5\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}2a+6b=10\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}7b=7\\2a-b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}\left(tm\right)}$

$\Rightarrow\hept{\begin{cases}2\sqrt{x}=2\\\frac{1}{y-1}=1\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\left(tm\right)$

Vậy ...

Đúng(0)

PT

Phùng Thị Uyên

4 tháng 6 2021

1,$\left\{{}\begin{matrix}2\sqrt{x}+\dfrac{3}{y-1}=5\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.$ ĐKXĐ:x≥o,y≠1

⇔$\left\{{}\begin{matrix}4\sqrt{x}+\dfrac{6}{y-1}=10\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{y-1}=7\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.$$\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=1\\4\sqrt{x}-\dfrac{1}{1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\4\sqrt{x}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\left(TM\right)$

vậy hpt đã cho có nghiệm duy nhất (x,y)=(1,2)

2,a, xét pthđgđ của (d) và (p) khi m=3:

x$^2$=3x-1⇔$x^2-3x+1=0$

Δ=(-3)$^2$-4.1.1=5>0

⇒pt có 2 nghiệm pb

$x_1=\dfrac{3+\sqrt{5}}{2}$ ,$x_2=\dfrac{3-\sqrt{5}}{2}$

thay x=x$_1$=$\dfrac{3+\sqrt{5}}{2}$ vào hs y=x$^2$ ta được:

y=($\dfrac{3+\sqrt{5}}{2}$)$^2$=$\dfrac{14+6\sqrt{5}}{4}$⇒A($\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}$)

thay x=x$_2$=$\dfrac{3-\sqrt{5}}{2}$ vào hs y=x$^2$ ta được:

y=$\left(\dfrac{3-\sqrt{5}}{2}\right)^2=\dfrac{14-6\sqrt{5}}{4}$⇒B($\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}$)

vậy tọa độ gđ của (d) và (p) là A($\dfrac{3+\sqrt{5}}{2},\dfrac{14+6\sqrt{5}}{4}$) và B ($\dfrac{3-\sqrt{5}}{2},\dfrac{14-6\sqrt{5}}{4}$)

b,xét pthđgđ của (d) và (p) :

$x^2=mx-1$⇔$x^2-mx+1=0$ (*)

Δ=(-m)$^2$-4.1.1=m$^2$-4

⇒pt có hai nghiệm pb⇔Δ>0

⇔m$^2$-4>0⇔m>16

với m>16 thì pt (*) luôn có hai nghiệm pb $x_1,x_2$

theo hệ thức Vi-ét ta có:

(I) $\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=1\end{matrix}\right.$

$x_1,x_2$ TM $x_2$(x$_1$$^2$+1)=3

⇒$x_2.x_1^2$+$x_2$=3⇔$x_2.x_1.x_1+x_2=3$⇔($x_2.x_1$)($x_1+x_2$)=3 (**)

thay (I) vào (**) ta được:

1.m=3⇔m=3 (TM m≠0)

vậy m=3 thì (d) cắt (p) tại hai điểm pb có hoanh độ $x_1.x_2$ TM $x_2$($x_1^2+1$)=3

Đúng(0)

KK

Kim Khánh Linh

18 tháng 5 2021 - olm

Tìm tọa độ giao điểm của parabol $(P)$: $y=2 x^{2}$ và đường thẳng $(d)$: $y=3 x-1$ bằng phép tính.

#Toán lớp 9

6

NH

Nguyễn Huy Tú

18 tháng 5 2021

Hoành độ giao điểm thoảng mãn pt :

$2x^2=3x-1\Leftrightarrow2x^2-3x+1=0$

$\Delta=9-8=1$

$x_1=\frac{3-1}{4}=\frac{1}{2};x_2=\frac{3+1}{4}=1$

Thay x = 1/2 vào (d) ta được : $y=\frac{3}{2}-1=\frac{1}{2}$

Thay x = 1 vào (d) ta được : $y=3-1=2$

Vậy tọa độ giao điểm của (P) và (d) là A ( 1/2 ; 1/2 ) ; B( 1 ; 2 )

Đúng(0)

ND

Ngọc Đan

18 tháng 5 2021

Tọa độ giao điểm 2 đthg: $2x^2$ =3x-1

<=>$2x^2$- 3x+1=0

Có dạng a+b+c=2-3+1=0

=>$x_1=1$ => y=2.$1^2$=2 =>tọa độ iao điểm(x;y)=(1;2)

$x_2=\frac{1}{2}$ =>y=2.$\left(\frac{1}{2}\right)^2$=1/2 =>tọa độ giao điẻm(x;y)=($\frac{1}{2}$;$\frac{1}{2}$)

Đúng(0)

NT

Nguyễn Thị Ánh Dương

19 tháng 5 2021 - olm

Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho tam...

Đọc tiếp

#Toán lớp 9

0

PL

Phuong Linh

6 tháng 6 2021

2. Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=X’ và đường thẳng (d):

y=3x+m² -1

a) Tìm m để đường thẳng (d) đi qua điểm A(-1: 5).

b) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x,,, thỏa

mãn |x|+2|x|=3.

#Toán lớp 9

0

NT

nguyễn thị thu thảo

10 tháng 12 2016

cho parabol p : y=-x và đường thẳng d : y= 2(m-1)x-(m+4). Cmr (P) luôn cắt (d) tại hai điểm phân biệt x₁và x₂ khi đó tìm m để -2<x₁<x₂

#Toán lớp 10

0

D

danh

31 tháng 8 2021

cho parabol (p) : y=$-\dfrac{x^2}{2}$và đường thẳng y=$-\dfrac{1}{2}x-1$ (d) trên cùng mặt tọa độ .a) vẽ parabol (P) và đường thẳng (d) trên cùng hệ trục tọa độ Oxy

b)tìm tọa độ giao điểm của (p) và (d) bằng phép tính

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

31 tháng 8 2021

b: Phương trình hoành độ giao điểm là:

$-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1$

$\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0$

$\Leftrightarrow x^2-x-2=0$

$\Leftrightarrow\left(x-2\right)\left(x+1\right)=0$

$\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.$

Thay x=2 vào (P), ta được:

$y=\dfrac{-2^2}{2}=-2$

Thay x=-1 vào (P), ta được:

$y=-\dfrac{1^2}{2}=-\dfrac{1}{2}$

Đúng(2)

TT

Thanh Trúc

13 tháng 4 2021

1) Giải hệ phương trình$\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.$2) Trong mặt phẳng tọa độ Oxy cho đường thẳng d : y = 3x + $m^2$ -1 và parabol (P) : y = $x^2$a) Chứng minh d luôn cắt (P) tại hai điểm phân biệt với mọi m.b) Gọi $x_1$ và $x_2$ là hoành độ các giao điểm của d và (P). Tìm m...

Đọc tiếp

#Toán lớp 9

2

NL

Nguyễn Lê Phước Thịnh

13 tháng 4 2021

Câu 1:

ĐKXĐ: $\left\{{}\begin{matrix}x\ne1\\y\ne-2\end{matrix}\right.$

Ta có: $\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2x-2+2}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{2}{x-1}+\dfrac{1}{y+2}=3\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{x-1}-\dfrac{4}{y+2}=8\\\dfrac{6}{x-1}+\dfrac{3}{y+2}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-7}{y+2}=-1\\\dfrac{6}{x-1}+\dfrac{3}{y+2}=9\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}y+2=7\\\dfrac{6}{x-1}+\dfrac{3}{7}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\\dfrac{6}{x-1}=\dfrac{60}{7}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}x-1=\dfrac{7}{10}\\y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{17}{10}\left(nhận\right)\\y=5\left(nhận\right)\end{matrix}\right.$

Vậy: Hệ phương trình có nghiệm duy nhất là $\left(x,y\right)=\left(\dfrac{17}{10};5\right)$

Đúng(1)

NL

Nguyễn Lê Phước Thịnh

13 tháng 4 2021

Câu 2:

a) Phương trình hoành độ giao điểm của (P) và (d) là:

$x^2=3x+m^2-1$

$\Leftrightarrow x^2-3x-m^2+1=0$

$\Delta=\left(-3\right)^2-4\cdot1\cdot\left(-m^2+1\right)$

$=9-4\left(-m^2+1\right)=9+4m^2-4=4m^2+5>0\forall m$

Vậy: (d) luôn cắt (P) tại hai điểm phân biệt với mọi m

Đúng(1)

T

⚚TᕼIêᑎ_ᒪý⁀ᶜᵘᵗᵉ

13 tháng 3 2023 - olm

Parabol $y=ax^2+bx+2$ đi qua điểm M ( 2 ; 3 ) và N ( -1 ; 4 ) có phương trình là :

A . $y=x^2+x+2$

B . $y=\dfrac{5}{6}x^2-\dfrac{7}{6}x+2$

C . $y=2x^2-\dfrac{7}{2}x+2$

D . $y=x^2-x+2$

#Toán lớp 9

1

MH

Minh Hiếu

13 tháng 3 2023

Ta có:

Prabol đi qua điểm M(2;3) và N(-1,4)

=> $\left\{{}\begin{matrix}4a+2b+2=3\\a-b+2=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}\\b=-\dfrac{7}{6}\end{matrix}\right.$

=> chọn B

Đúng(2)

TC

Thầy Cao Đô

Giáo viên VIP

9 tháng 5 2022 - olm

(2 điểm) 1) Giải hệ phương trình $\left\{\begin{aligned}&\dfrac{3}{x+1}-2 y=-1 \\ &\dfrac{5}{x+1}+3 y=11\end{aligned}\right.$.

2) Trong mặt phẳng toạ độ $O x y$, cho parabol $(P)$: $y=x^{2}$ và đường thẳng $(d)$: $y=2 x+m-2$. Tìm tất cả giá trị của $m$ để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_{1},$ $x_{2}$ sao cho $\left|x_{1}-x_{2}\right|=2$.

#Toán lớp 9

2

NH

Nguyễn Huy Tú

9 tháng 5 2022

Hoành độ giao điểm (P) ; (d) tm pt

$x^2-2x-m+2=0$

$\Delta'=1-\left(-m+2\right)=m+3$

Để (P) cắt (d) tại 2 điểm pb khi m > -3

Theo Vi et $\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m+2\end{matrix}\right.$

Ta có $\left(x_1-x_2\right)^2=4\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4$

Thay vào ta được $4+4\left(m-2\right)=4\Leftrightarrow4m-4=4\Leftrightarrow m=2$(tm)

Đúng(1)

NH

Nguyễn Huy Tú

9 tháng 5 2022

$\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=-19\\y=\dfrac{\dfrac{3}{x+1}+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.$

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP